


Next: Specification of Quantum
Up: Notes on Quantum States
Previous: Notes on Quantum States
In classical mechanics, the state of a system may be specified by
giving the coordinates 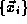 and velocities
and velocities 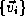 of all
of the particles in the system. Once this is done, all measurable
quantities such as the momenta
of all
of the particles in the system. Once this is done, all measurable
quantities such as the momenta 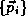 , total energy
, total energy 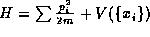 and angular momentum
and angular momentum 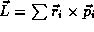 of the system may be determined. Such
measurable quantities are known as observables. Under the classical
principle of determinism, once the state of the system is specified at
time t = 0, the laws of motion may be solved to determine the state
of the system
of the system may be determined. Such
measurable quantities are known as observables. Under the classical
principle of determinism, once the state of the system is specified at
time t = 0, the laws of motion may be solved to determine the state
of the system 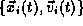 for all later times.
for all later times.
The situation in quantum mechanics is not much different. We may
still make measurements of the familiar physical observables mentioned
above (and some new ones such as spin or polarization which we will
learn about later). As we have seen in our discussions of the
uncertainty principle and interference experiments, although the
results of individual measurements are unpredictable on the
quantum scale, measurements on a system in a given state yield a
well-defined distribution of results. If we simply accept this
notion and generalize our concept of ``experiment" to the procedure of
determining the distribution associated with many measurements of the
same observable over a set of identically prepared systems, then we
may maintain the idea that the quantum state of a system
determines the results of all experiments measuring physical
observables.
As we shall refer to the quantum state of a system often, we shall
make a special symbol for it, 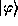 . The symbol
. The symbol
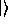 is called a ``ket.'' We may place different symbols inside
the ket to distinguish different states. For instance, our system may
be in the state
is called a ``ket.'' We may place different symbols inside
the ket to distinguish different states. For instance, our system may
be in the state 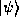 at time t = 0 and in the state
at time t = 0 and in the state
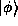 at some later time.
at some later time.
Keep in mind that, in general, 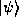 does not determine
the result of any individual measurement of an observable, only
probability distributions such as
does not determine
the result of any individual measurement of an observable, only
probability distributions such as 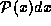 , the probability of
finding a particle with position x in the range
, the probability of
finding a particle with position x in the range 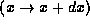 , or
, or
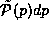 , the probability of finding the momentum of the
particle in the range
, the probability of finding the momentum of the
particle in the range 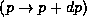 . In the case of photons we may
also consider the observable of spin or polarization and measure
. In the case of photons we may
also consider the observable of spin or polarization and measure 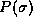 , the probability of observing a right
, the probability of observing a right 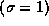 or
left
or
left 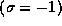 circularly polarized photon.
circularly polarized photon.
We mention the polarization of photons above to underscore the fact
that we will keep the abstract portion of our discussion completely
general. For the most part of the course, however, we will focus on
systems of single particles which have no internal structure so that
we will concern ourselves with only the observables of position 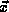 , momentum
, momentum 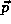 and those observables which may be derived from these
two, such as energy
and those observables which may be derived from these
two, such as energy 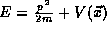 and angular
momentum
and angular
momentum 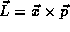 .
.



Next: Specification of Quantum
Up: Notes on Quantum States
Previous: Notes on Quantum States
Prof. Tomas Alberto Arias
Wed Oct 11 21:10:55 EDT 1995
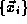 and velocities
and velocities 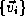 of all
of the particles in the system. Once this is done, all measurable
quantities such as the momenta
of all
of the particles in the system. Once this is done, all measurable
quantities such as the momenta 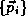 , total energy
, total energy 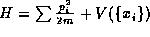 and angular momentum
and angular momentum 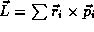 of the system may be determined. Such
measurable quantities are known as observables. Under the classical
principle of determinism, once the state of the system is specified at
time t = 0, the laws of motion may be solved to determine the state
of the system
of the system may be determined. Such
measurable quantities are known as observables. Under the classical
principle of determinism, once the state of the system is specified at
time t = 0, the laws of motion may be solved to determine the state
of the system 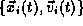 for all later times.
for all later times.
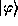 . The symbol
. The symbol
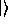 is called a ``ket.'' We may place different symbols inside
the ket to distinguish different states. For instance, our system may
be in the state
is called a ``ket.'' We may place different symbols inside
the ket to distinguish different states. For instance, our system may
be in the state 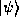 at time t = 0 and in the state
at time t = 0 and in the state
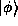 at some later time.
at some later time.
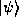 does not determine
the result of any individual measurement of an observable, only
probability distributions such as
does not determine
the result of any individual measurement of an observable, only
probability distributions such as 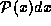 , the probability of
finding a particle with position x in the range
, the probability of
finding a particle with position x in the range 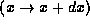 , or
, or
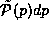 , the probability of finding the momentum of the
particle in the range
, the probability of finding the momentum of the
particle in the range 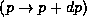 . In the case of photons we may
also consider the observable of spin or polarization and measure
. In the case of photons we may
also consider the observable of spin or polarization and measure 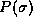 , the probability of observing a right
, the probability of observing a right 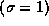 or
left
or
left 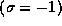 circularly polarized photon.
circularly polarized photon.
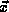 , momentum
, momentum 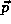 and those observables which may be derived from these
two, such as energy
and those observables which may be derived from these
two, such as energy 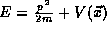 and angular
momentum
and angular
momentum 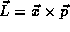 .
.