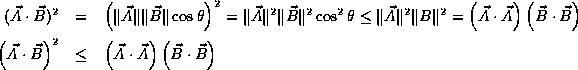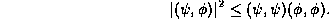Next: About this document
Up: Principle of Superposition
Previous: Parseval's Theorem: Fourier
As we have seen, 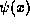 is sufficient to compute the distributions
for
position
is sufficient to compute the distributions
for
position 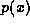 and momentum
and momentum 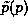 through (3), (13) and (14)
and
thus is sufficient to specify or represent the quantum state
through (3), (13) and (14)
and
thus is sufficient to specify or represent the quantum state
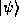 of a system where x and p are the only basic
observables.
However, through (12) and (13) we see that
of a system where x and p are the only basic
observables.
However, through (12) and (13) we see that
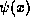 and
and 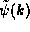 provide equivalent information and so
either
is an equally valid way of representing the state
provide equivalent information and so
either
is an equally valid way of representing the state 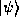 . If we
wish, we can, in principle, compute all of our physical quantities using
. If we
wish, we can, in principle, compute all of our physical quantities using
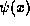 in the position representation, or using
in the position representation, or using 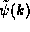 in the momentum representation and get equally valid results.
in the momentum representation and get equally valid results.
We have already seen an example of this in Parseval's Theorem. We may
compute the Hermitian Inner product between two states
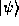 and
and 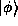 , either in the position or momentum
representation and get the same result
, either in the position or momentum
representation and get the same result
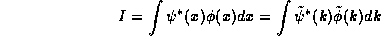
Because this quantity is the same regardless of which representation
we choose, it depends only on the states 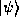 and
and
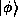 and we thus give it a special symbol independent of the
choice of representation to remind us of this fact
and we thus give it a special symbol independent of the
choice of representation to remind us of this fact
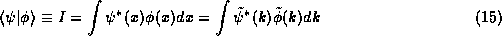
When we write 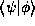 it is clear what is meant. To
evaluate it, the reader is responsible for picking a convenient
representation of his own choosing and then performing the
appropriate integration in (15).
it is clear what is meant. To
evaluate it, the reader is responsible for picking a convenient
representation of his own choosing and then performing the
appropriate integration in (15).
The Hermitian Inner product integral itself has many interesting
mathematical
properties and so it is useful to have a notation for it as well.
We shall write
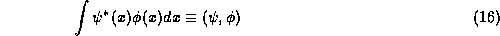
and
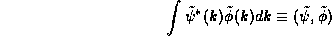
So that 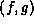 just means form the product
just means form the product 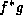 of the two
functions and integrate over their argument. (15) then is written
compactly as
of the two
functions and integrate over their argument. (15) then is written
compactly as
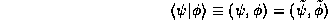
We note that the mathematical structure of the Hermitian Inner product
(16)
as a sum over the product of values taken from two ``lists'' is
very similar to that of the dot product between two vectors
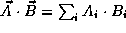 . It is therefore not
surprising that they share many properties. The most important of these
(whose proof we defer to problem set 6) is the Cauchy-Schwartz
inequality.
For vectors we have
. It is therefore not
surprising that they share many properties. The most important of these
(whose proof we defer to problem set 6) is the Cauchy-Schwartz
inequality.
For vectors we have
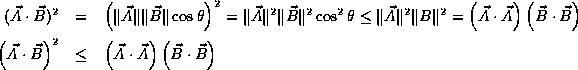
For the Hermitian Inner product, you will prove
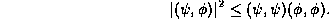



Next: About this document
Up: Principle of Superposition
Previous: Parseval's Theorem: Fourier
Prof. Tomas Alberto Arias
Wed Oct 11 21:10:55 EDT 1995
 is sufficient to compute the distributions
for
position
is sufficient to compute the distributions
for
position  and momentum
and momentum 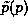 through (3), (13) and (14)
and
thus is sufficient to specify or represent the quantum state
through (3), (13) and (14)
and
thus is sufficient to specify or represent the quantum state
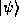 of a system where x and p are the only basic
observables.
However, through (12) and (13) we see that
of a system where x and p are the only basic
observables.
However, through (12) and (13) we see that
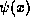 and
and 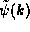 provide equivalent information and so
either
is an equally valid way of representing the state
provide equivalent information and so
either
is an equally valid way of representing the state 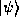 . If we
wish, we can, in principle, compute all of our physical quantities using
. If we
wish, we can, in principle, compute all of our physical quantities using
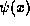 in the position representation, or using
in the position representation, or using 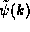 in the momentum representation and get equally valid results.
in the momentum representation and get equally valid results.
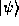 and
and 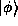 , either in the position or momentum
representation and get the same result
, either in the position or momentum
representation and get the same result
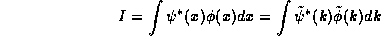
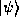 and
and
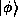 and we thus give it a special symbol independent of the
choice of representation to remind us of this fact
and we thus give it a special symbol independent of the
choice of representation to remind us of this fact
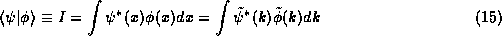
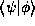 it is clear what is meant. To
evaluate it, the reader is responsible for picking a convenient
representation of his own choosing and then performing the
appropriate integration in (15).
it is clear what is meant. To
evaluate it, the reader is responsible for picking a convenient
representation of his own choosing and then performing the
appropriate integration in (15).
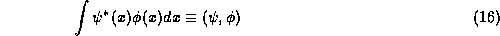
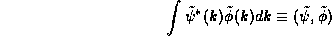
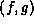 just means form the product
just means form the product 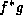 of the two
functions and integrate over their argument. (15) then is written
compactly as
of the two
functions and integrate over their argument. (15) then is written
compactly as
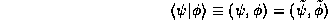
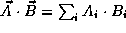 . It is therefore not
surprising that they share many properties. The most important of these
(whose proof we defer to problem set 6) is the Cauchy-Schwartz
inequality.
For vectors we have
. It is therefore not
surprising that they share many properties. The most important of these
(whose proof we defer to problem set 6) is the Cauchy-Schwartz
inequality.
For vectors we have