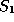 and
and 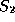 which you are told produce
photons in two (possibly different) quantum states A and B.
Answer the following questions based on our discussion in
lecture about quantum states. Give a brief explanation of
your answers.
which you are told produce
photons in two (possibly different) quantum states A and B.
Answer the following questions based on our discussion in
lecture about quantum states. Give a brief explanation of
your answers.
As mentioned in lecture, electromagnetic waves of a given wave-vector can be in one of two independent modes or ``polarizations.'' For an electromagnetic wave propagating along the z direction in free space, Maxwell's equations show that the electric field vector associated with this wave must point in the plane perpendicular to the z direction of propagation. If, as the wave passes, the electric field oscillates up and down along the x direction, the wave is considered x-polarized. If the electric field oscillates along the y direction, the wave is considered y-polarized. Superposing waves of these two types of polarization can result in a right circularly polarized wave r, where the electric field moves in counter-clockwise circles as the wave passes or in a left circularly polarized wave l where the field moves in clockwise circles as the wave passes. Filters exist which pass either only x, y, r or l polarized waves. You may wish to refer to chapter six of French and Taylor for a more detailed discussion of polarization, although this problem is designed so that everything you need to answer the questions below should be found in the lecture notes and in the statement of this problem.
We know that light is composed of photons and so the classical
observable of polarization must make up part of the description of the
quantum state of the photon. Imagine that you are given a
polarization filter of the type x indicated above and are presented
with two sources of light 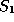 and
and 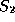 which you are told produce
photons in two (possibly different) quantum states A and B.
Answer the following questions based on our discussion in
lecture about quantum states. Give a brief explanation of
your answers.
which you are told produce
photons in two (possibly different) quantum states A and B.
Answer the following questions based on our discussion in
lecture about quantum states. Give a brief explanation of
your answers.