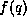 and
and 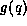 to be given by
to be given by
In lecture we defined the Hermitian inner product between two
functions 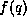 and
and 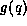 to be given by
to be given by
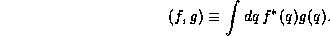
We also noted that this operation is very analogous to the familiar vector dot product

Demonstrate that the following properties hold for the
Hermitian inner product and state the analogous
property for the vector dot product. In the statements below f,
g and h will be functions, whereas lower case greek letters will be
constants, so that, for instance, 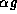 means
means 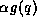 .
.
Mathematicians call any operation 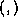 holding the four properties
listed below a Hermitian inner product. Because mathematicians take
great care in their definitions, most of the properties of the
operation we have defined for
holding the four properties
listed below a Hermitian inner product. Because mathematicians take
great care in their definitions, most of the properties of the
operation we have defined for 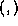 follow from just these four basic
properties. You may then use as a guide for any proofs you may
need to give involving the Hermitian inner product. Because they are
so analogous to the properties of the ordinary vector inner product,
these relations should be easy to remember.
follow from just these four basic
properties. You may then use as a guide for any proofs you may
need to give involving the Hermitian inner product. Because they are
so analogous to the properties of the ordinary vector inner product,
these relations should be easy to remember.