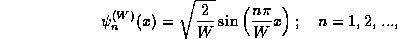
In this problem you will need to use the functional form for the eigenstates of a particle of mass m in a rigid ``box'' (infinite square-well potential) of width W. Properly normalized, these wavefunctions are
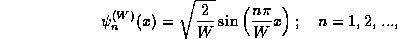
with energies
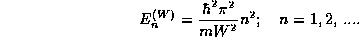
Now imagine a particle of mass m in the ground state,
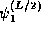, in an infinite well of width 
. (You might
imagine preparing this state by putting the particle in the well and
then waiting a very long time for it to radiate away all of its excess
energy.) Suddenly, the right wall of the well is moved from 
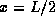to x=L, and the energy of the particle is measured immediately,
before the quantum state of the particle has an opportunity to respond
to the sudden change in the environment.