In this problem, you will analyze the consequences of the de Broglie relations (i.e., Bohr quantization) on the motion of ``conical pendulum'' attached to a spring (see figure). This system is like a normal pendulum, there is a mass m suspended from a point S and feeling the force of gravity mg directed downward.
There are two important differences from the normal pendulum, however. First, the mass is free to move in anyway about the point S and make circular orbits of radius R as indicated in the figure. Second, the mass is not only connected to the point S with a rigid string but also to the rotation axis with with a spring with spring constant k and natural length zero. The force from the spring is thus directed radially inward with magnitude kR.
For reference, we will call the momentum of the particle p, the
angle which the rod L makes with the direction of the vertical
, the distance from the mass m to the vertical line R, the
total energy (kinetic plus potential) of the pendulum E, and the
period when the particle undergoes circular motion T. In the Bohr
analysis of the motion there must be an integral number n of de
Broglie wavelengths around the circumference of the orbit of radius
R. In a quantum state n, there are specific values allowed to the
angle and energy of the system, which we shall call 
, and
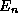, respectively. Your task is to use the Bohr quantization
condition to compute 
and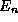 
, and understand the behavior
of the level spacings in the spectrum 
by using the
correspondence principle.