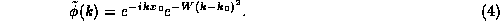
Consider a new function with the following Fourier transform,
For concreteness, imagine that this wavefunction represents the
momentum of photons in a detector used to measure electrons in the
state described by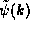 
. After interacting with the photons
in the detector, the electrons of initial momenta k will have new
momenta given by 
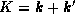where is 
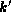is the momentum of the photon
with which each electron interacted. After adding up all possible
interactions, the new wavefunction of the electrons after measurement
will be
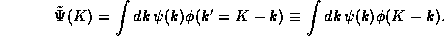
This operation is known as the convolution
and is written symbolically as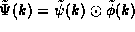 
.
Confirm, within this example, the Fourier Convolution
Theorem:
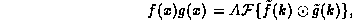
where A is a constant fixed for all functions f,g. Use your
result to determine what the value of this constant must
be. We have already descrbed the effects of the measurement process
on the momentum distribution. Now, considering especially the limit
W << D,
explain in words the effect of the measurement process on
the probability distribution of finding the electrons at different
points in space.
Hint: This part will involve more Gaussian integration.
