
Another property of the Hermitian inner product which has a simple vector dot product analogue is the Schwartz Inequality,

This property is slightly more difficult to prove, but is useful in showing the uncertainty principle.
This result is also the crucial lemma in our coming rigorous proof of the Heisenberg Uncertainty Principle! It is well worth the time understanding the proof.
Prove the Schwartz inequality for the Hermitian inner
product in a way different than on last year's problem set. The proof
from last year's problem set will not be accepted.
Hint: First explain
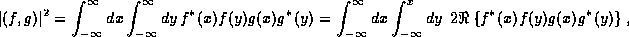
where  is defined to be the real part of the
complex number z. Then, perform a similar operation for the left
hand side and compare your results.
is defined to be the real part of the
complex number z. Then, perform a similar operation for the left
hand side and compare your results.