Study Guide for Final Examination

Massachusetts Institute of Technology

Department of Physics

Physics 8.04 May 18, 1997

The material which the final examination will cover includes the material covered on the first and second quizzes as well as bound state solutions for the Dirac -function and the one dimensional simple harmonic oscillator, and scattering problems in one dimension including computing reflection and transmission probabilities and packet delay times for sharp potential steps, resonant transmission across a barrier, tunneling through a barrier, and resonant tunneling through a double barrier, and scattering problems involving -potentials.

The material covered on the final includes but need not be limited to the material in the outline below.

Quantum Theory: a fundamental description of the behavior of matter and energy

1. Experiments establishing the identity/nature of the building blocks of the microscopic world
   1. Nuclei -- Rutherford Scattering
   2. Electrons ( )
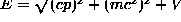      1. J.J. Thomson's, 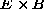experiment 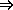measure e/m
      2. R.A. Millikan's oil drop experiment 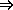measure e
      3. Davisson-Germer/G.P. Thomson Experiments 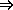wave-like nature of electrons with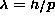
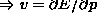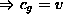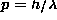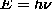      4. Classical mechanics ( ) + correspondence principle ( ) leads to the De Broglie Hypotheses, and . From this argument we see why both the energy-frequency and the wavelength-momentum h's are the same and why the h's are the same for all objects.
      5. Double-slit thought-experiments ( interference patterns) + the discreteness of microscopic events leads to the idea that microscopic events are probabilistic in nature but with a predictable distribution. We find that the probability of an event 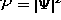is the complex magnitude squared of a wave-like amplitude. The amplitude function 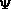somehow senses and propagates through the entire system including any apparatus making observations of the system.
      6. Single-slit thought-experiments lead to the Heisenberg Uncertainty Principle [HUP] as a basic property of matter: 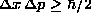. Applications of HUP:
         • Limits on the predictability of classical trajectories: quantum pin-ball
         • Ground state energies: Particle in a box: 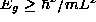(energy of confinement) Simple harmonic oscillator [SHO]: 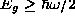Hydrogen Atom [H-atom]: 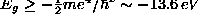(explains stability, size and energy of atoms)
   3. Photons
      1. A. Einstein, photoelectric effect
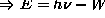
      2. Inverse photoelectric effect Bremsstrahlung/X-ray-emission
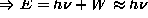
      3. GI Taylor: single-photon interference experiments showing the probabilistic nature of the arrival of individual photons.
      4. Classical E&M experiments (Maxwell's equations 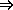E=cp) + Correspondence Principle ( 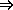large numbers of photons en masse act like classical E&M) and Planck's relation ( 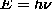) leads to the conjecture that 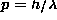for photons as well as for particles

2. Putting the building blocks together
   1. Compton Scattering 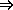confirms 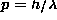experimentally
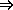
   2. Atomic Spectra: Balmer Series, etc. 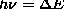with 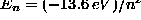. 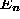may be understood with Bohr's quantization condition 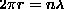. To get perfect alignment with the experiments must use the effective mass !
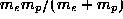      1. Franck-Hertz 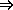verification of existence of discrete internal energy states
      2. Mosely's X-ray spectra of multi-electron atoms 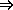basic concepts work if a shell-structure is assumed for the electrons
      3. Closer Look at Semiclassical Quantization
         1. Quantization condition: ,
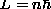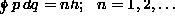
         2. Examples:
            • Particle in a box:
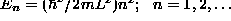
            • Simple Harmonic Oscillator [SHO]:
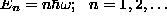
            • Hydrogen Atom [H-atom]:
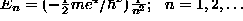
         3. Correspondence Principle/Classical Limit
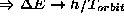
3. de Broglie Hypothesis:

   An electron or photon represents the possibility for the occurrence of a discrete microscopic event, where the probability of that event may be described by a superposition of waves with frequency 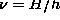and wavelength 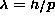, where H is the Hamiltonian, p is the momentum for the electron or photon, and h is Planck's constant

4. Quantum States and Observables
   1. Quantum State -- two systems are defined as being in the same quantum state if and only if the statistical results of all experiments carried out on those systems are identical.
   2. Pure Quantum State -- a system is in a pure quantum state with respect to an observable if all measurements of that observable always yield the same value.
   3. Specification of Quantum States -- specifying the probability distribution for just one observable is, in general, insufficient to specify the quantum state of a system.
   4. Representation of Quantum States -- the set of quantum amplitudes (either 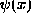for all x, 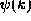for all k, or 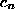for all n) in a particular representation (position, momentum, energy) are sufficient to specify a quantum state. Students should be able to transform readily between different representations.
5. Distributions, Averages and Operators
   1. The probability of measuring a particular value of a particular observable is given by the complex magnitude squared of the quantum amplitude in that representation. , , .
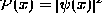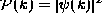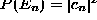   2. Averages may be computed directly from the probability distributions (e.g., 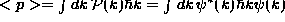) or through use of the appropriate operators .
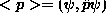   3. Students should be comfortable with the use of the Hermitian inner product 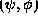and basic operator operations such as 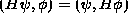or .
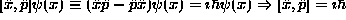   4. Students should be able to apply the ``Quantum Purity Test'' to determine whether a quantum state is pure with respect to a particular observable by applying the corresponding operator: .

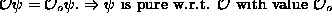6. Time Dependent Schrödinger Equation (TDSE)
   1. Students should be familiar with the origins and form of the TDSE.
   2. Students should be familiar with and able to apply the conservation of probability, the continuity equation and the probability current.
   3. Students should be familiar with and able to apply Ehrenfest's theorem, both in the case of 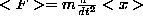and in its general form 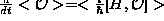for any operator .
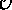   4. Students should be familiar with and able to apply the formal solution to the TDSE:

      

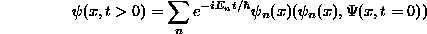
7. Time Independent Schrödinger Equation (TISE)
   1. Students should recognize the TISE as the quantum purity test for pure states of energy.
   2. Students should be familiar with the expansion 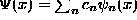and be able to determine the constants 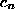for any given function 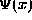through the relation .
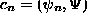   3. Students should be familiar with orthonormality among eigenstates .
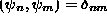   4. Students should be able to complete proofs using the expansions, 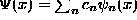and .
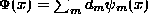   5. Given a wavefunction expanded at t=0, 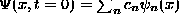, students should be able to give the solution for all later times .
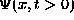   6. Students should be able to give qualitative sketches of bound state solutions to the TISE.

8. Applications of the TDSE
   • Students should be able to use the TDSE and the Method of Stationary Phase to describe the behavior of wave packets in scattering problems, including being able to locate the positions of the source, reflected and transmitted packets in terms of a) the phases of the linear combination coefficients making up the wave packet and b) the phases of the quantum amplitudes for the source, reflected and transmitted beams.

9. Applications of the TISE
   1. Students should be able to solve analytically for the bound eigenenergies and eigenstates of the TISE in one dimensional problems involving piecewise-constant potentials and Dirac -functions.
   2. Students should be able to reproduce each step of the solution for the simple harmonic oscillator. This includes:
      • The conversion to a dimensionless equation without the constants , m, and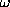
      • Knowing the form of the solution as as a product of polynomials times a Gaussian which is its own Fourier transform:
        
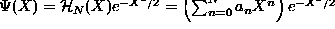
      • The generation of the equation for the polynomials:
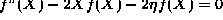
      • The solution of the above equation using the power series expansion:
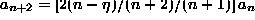
      • Reconstructing the eigenstates and applying the solutions as on the problem sets
      • Students should also be familiar with generating sucessive excited states using the creation operator 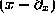, and also the fact that 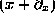is the annihilation operator, which produces the next lower state when applied to a pure state of the SHO.
   3. Students should be able to solve analytically for the scattering eigenstates of the TISE in one-dimensional problems involving piecewise-constant potentials and Dirac -functions. They should be able to interpret the results and from them to extract the quantum amplitudes of transmission t(k) and reflection r(k). 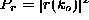From these amplitudes, students should be able to compute reflection and transmission probabilities ( and 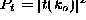, respectively) and delay times ( 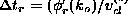and 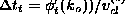, where 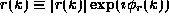, , 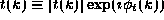and 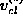is the classical velocity in the region which is the source of the scattered particles.
   4. Students should be familiar with the following scattering phenomena:
      • Reflection from a sudden change potential:
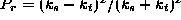
      • Barrier penetration: the probability is non-zero in a forbidden region but decays exponential with a decay constant 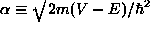. For such situations there is a time delay in the generation of the reflection of 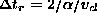, as though the particles first travel a distance 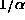into the barrier and then the same distance back out.
      • Resonant scattering across a potential well: sometimes 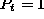for special values of k
      • Resonant tunneling: sometimes 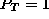even when tunneling is involved so long as there is a resonance region separated by two symmetric, opposing scatterers
10. Feynman diagrams: Students should be able to perform Feynman sums over histories to solve scattering problems. This includes
    • Listing the histories using diagrams
    • Writing the quantum amplitude for each history in terms of the amplitudes for the fundamental events in the history
    • Summing the resulting geometric series
    • Knowing how to determine the quantum amplitudes for fundamental events such as propagation in classically allowed regions ( ) and classically forbidden regions ( ) and for scattering events (r and t) from potential steps and -functions.
    • Realizing that the resulting quantum amplitudes are precisely the same prefactors that would be obtained from solving the traditional Schrödinger Equation using exponential terms properly centered at the edges of the scattering region.

• About this document ...

Postscript Version