Background: In lecture we explored the representations for quantum state of the system corresponding to the observables of position x and momentum p. We used these representations to derive the forms for operators for position and momentum in both the position and momentum representations. There are more than these two representations for a quantum state. By the quantum principle of superposition, we expect there to be a representation for each physical observable. The observable of energy is no exception to this. In this problem, you will practice the skills developed in lecture for dealing with different representation, but now in a new context.
You will also find that the energy representation is useful for proving many theorems about the time development of quantum states. This is a result of the close relationship between energy and time.
This problem will discuss both general considerations and a specific
example. For the general considerations in this problem, we begin by
using the principle of superposition to write any quantum state,
or 
, in terms of the pure states of energy as
Here, the pure states
are given by 
and are properly normalized so that
.
For the specific considerations, we use use the energy states of the Infinite Square Well of length L, which are given by
with energies
where here the Hamiltonian operator is just 
.
At times we will also use the (properly normalized) wave function
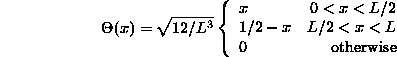
Assignment: