


Next: About this document
Massachusetts Institute of Technology
Department of Physics
Physics 8.04, Spring 1997February 5, 1997
Quantum Physics I, Spring 1997
Note: The notations in square brackets give chapter and section
readings roughly corresponding to the material in the outline. The
abbreviations are RH = Resnick and Halliday (section numbers), G
= Gasiorowicz (read section(s) contained with in given range of pages),
H = Heisenberg (section numbers), FT = French and Taylor
(section numbers), CN = class notes given out in lecture and provided
on the web.
Many thanks to Dicle Yesilleten (U'97) for her help, which was
invaluable in the production of this syllabus.
Syllabus
- I. Overview: Following the Scientific Method
- II. The Experimental Evidence
- A. Identity of the Basic Building Blocks of the World Around Us
- 1. Electrons (JJ Thomson/RA Millikan) [FT 1.3-1.4, H I2a]
- 2. Nuclei (E. Rutherford) [RH 7.1-7.3]
- 3. Electromagnetic Energy/Radiation (comment)
- B. Behavior of the Building Blocks
- 1. Nuclei (comment)
- 2. Electromagnetic Energy
- Classical E&M (recall)
- Photoelectric Effect (A Einstein) and related effects
[RH 5.1-5.3, 5.6, G 9]
- Single slit experiments (GI Taylor)
- Poisson statistics [CN ``Statistics'']
- Compton Scattering [RH 5.4, H I2d, G 11]
- 3. Electrons
- JJ Thomson (recall)
- Davisson-Germer Interference [CN ``de Broglie,'' RH 6.2, H I2b-c, G 13-15]
- GP Thomson Interference
- III. Exploration of Qualitative and Semiquantitative Pictures
- A. de Broglie Hypothesis [CN ``de Broglie'']
- B. Heisenberg Uncertainty Principle (HUP) [RH 6.5-6.7, CN ``HUP'', H II, G 33-38]
- Energy of the Hydrogen atom [CN ``HUP'']
- Atomic Spectra [RH 7.4]
- Franck-Hertz Experiment [RH 4.7, H I2e]
- C. Semiclassical Quantization and the Correspondence Principle [CN ``Bohr-Sommerfeld,'' [RH 7.7, 7.5, G 15-21]
- X-ray Spectra (Moseley) [FT 1.10]
- IV. Constructing a Quantitative Theory Consistent with the Experimental Evidence
- A. ``Kinematics'': The Wavefunction/Operator Framework [H IV3]
- 1. Wavefunctions/Fourier Transforms [CN ``States and Observables'']
- 2. Operators [CN ``Quantum Operators'', G 45-46, 114-118]
- B. ``Dynamics'': Time-Dependent Schrödinger Equation
(TDSE) [CN ``TDSE'', G 49-50]
- 1. Verify consistency with probabilistic interpretation:
probability currents, [CN ``TDSE'', G 42-45]
- 2. Verify consistency with the correspondence principle: Ehrenfest's Theorem, [G 125-127]
- 3. Computer solutions as examples
- V. Tools to Apply the Theory: Solving the TDSE
- A. Separation of Variables: Reduction to Time-Independent Schrödinger Equation (TISE) [CN ``TISE'']
- B. Time Independent Schrödinger Equation [CN ``TISE'']
- Qualitative solutions (1d) [FT 3.11]
- VI. Predictions of the Theory: Solutions to Schrödinger's Equation
- A. Scattering States in One Dimension [CN ``Scattering'']
- 1. Wave packets [G 27-31]
- Gaussian packet
- General Packet and Stationary phase
- 2. Reflection at a step/time delay, [G 74-85, 86-89]
- 3. Feynman diagrams and sum over histories
- 4. Symmetry and resonance
- B. Bound States in One Dimension
- 1. General features - eigenstate expansions, energy representation [CN ``TISE'', G 60-63]
- 2. Piecewise constant potentials [CN ``Finite Square Well'', [G 58, 67-70, 89-93]
- 3.
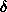 -function potential [G 93-99]
-function potential [G 93-99]
- 4. Simple Harmonic Oscillator [CN ``SHO'', G 103-108]
- dimensional analysis
- momentum representation/self-transform property of solutions
- full power series solution



Next: About this document
Prof. Tomas Alberto Arias
Wed Feb 5 13:52:46 EST 1997
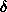 -function potential [G 93-99]
-function potential [G 93-99]