Figure 1: Quantized levels of charge

Figure 1: Quantized levels of charge
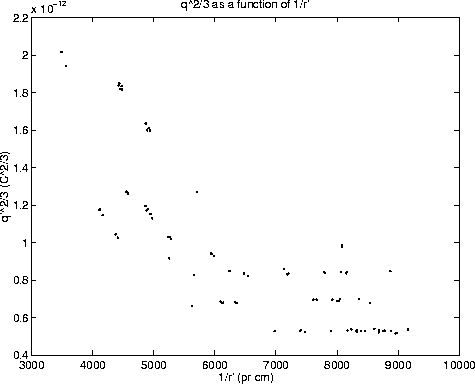
Figure 1 shows ![]() as a function of 1/r'.
The plot clearly indicates the quantization of charge, because
only certain 'levels' in the values of
as a function of 1/r'.
The plot clearly indicates the quantization of charge, because
only certain 'levels' in the values of ![]() are seen. The
problem for the further analysis is assigning a specific
number of elementary charges to each of the lines (determining n in
equation 8), so that
are seen. The
problem for the further analysis is assigning a specific
number of elementary charges to each of the lines (determining n in
equation 8), so that ![]() can
be determined from
can
be determined from ![]() . Assigning the quantum numbers is
the essence of he whole experiment, because that directly yields the
quantization of charge.
. Assigning the quantum numbers is
the essence of he whole experiment, because that directly yields the
quantization of charge.
A naive approach to this step would be to assign n=1 to the lowest level.
However, the magnitude of the elementary charge may very well be
so small that the electric field of the capacitor plates would be too weak
to overcome the gravitational pull on droplets of the size involved in this
experiment. A better approach is to estimate an average ![]() of the
lowest line, and also to look at the average spacing between the proceeding
lines. Since
of the
lowest line, and also to look at the average spacing between the proceeding
lines. Since ![]() is approximately twice as big as the spacing between
the consecutive lines, it is fair to assume that q' on the lowest level
corresponds to 2e'. Thus the quantum number 3,4..... can then be assigned to
the consecutive lines. By dividing through with the determined quantum numbers,
the graph in figure 2 is obtained. In the graph, lines with
is approximately twice as big as the spacing between
the consecutive lines, it is fair to assume that q' on the lowest level
corresponds to 2e'. Thus the quantum number 3,4..... can then be assigned to
the consecutive lines. By dividing through with the determined quantum numbers,
the graph in figure 2 is obtained. In the graph, lines with ![]() have
been omitted, because uncertainties don't make the lines as distinct as
they ideally should be. Thus, even though the lines are not clearly
separated, they would, if they were included, contribute to determining the
elementary charge without showing any indication of such an elementary charge
themselves.
have
been omitted, because uncertainties don't make the lines as distinct as
they ideally should be. Thus, even though the lines are not clearly
separated, they would, if they were included, contribute to determining the
elementary charge without showing any indication of such an elementary charge
themselves.
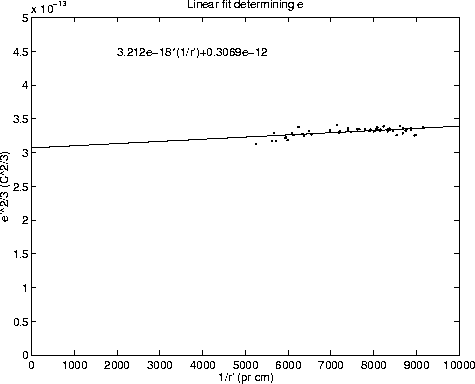
Figure 2: Linear fit yielding the elementary charge
By fitting a line to the points in figure 2 and extrapolating it to
![]() , the value
, the value ![]() is obtained. The main
sources of error associated with this number are estimated to be:
2% uncertainty in the voltage across the capacitor plates, 1% uncertainty
in the viscosity due to variations in the temperature, 2% uncertainty
in the timing of the motion and 2% uncertainty
due to the fit itself. Since all these parameters enter the formula for
is obtained. The main
sources of error associated with this number are estimated to be:
2% uncertainty in the voltage across the capacitor plates, 1% uncertainty
in the viscosity due to variations in the temperature, 2% uncertainty
in the timing of the motion and 2% uncertainty
due to the fit itself. Since all these parameters enter the formula for
![]() (equation 7) in the first order, the total uncertainty
is found by taking:
(equation 7) in the first order, the total uncertainty
is found by taking:
![]()
To get the value for e the value obtained by the fit must be raised to the
3/2 power. This also multiplies the error with a factor 1.5,
giving a total error of ![]() The following value for the elementary charge is thus obtained:
The following value for the elementary charge is thus obtained:
![]()
The experimental value is in agreement with the
tabulated value, ![]() .
.