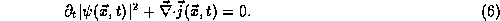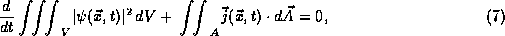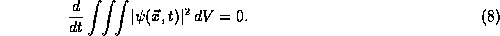Next: Supplemental note on
Up: Conservation of Probability
Previous: Global Conservation
We will now use a very general procedure to show that probability is
conserved under the dynamics given by the TDSE. By conservation of
probability we mean the requirement that the integral of 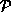 will
remain properly normalized
will
remain properly normalized 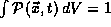 for all time t>0.
The procedure we are about to use is very general. It is used, for
instance, to show that energy and momentum are conserved in
electrodynamics under Maxwell's equations and that mass and momentum
are conserved under the equations of Newtonian fluid flow.
for all time t>0.
The procedure we are about to use is very general. It is used, for
instance, to show that energy and momentum are conserved in
electrodynamics under Maxwell's equations and that mass and momentum
are conserved under the equations of Newtonian fluid flow.
As we saw in the previous section the mathematical condition that
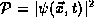 be conserved is that it obey the
continuity equation with no source term (
be conserved is that it obey the
continuity equation with no source term (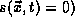 as
as
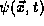 evolves according to the TDSE. To demonstrate
conservation all that we must now do is identify a probability
current density
evolves according to the TDSE. To demonstrate
conservation all that we must now do is identify a probability
current density 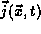 so that
so that 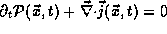 .
.
To identify this current density, we begin with the time derivative
in the equation of continuity (3) and then employ our
knowledge of the time derivatives of 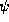 through the TDSE (2),
through the TDSE (2),
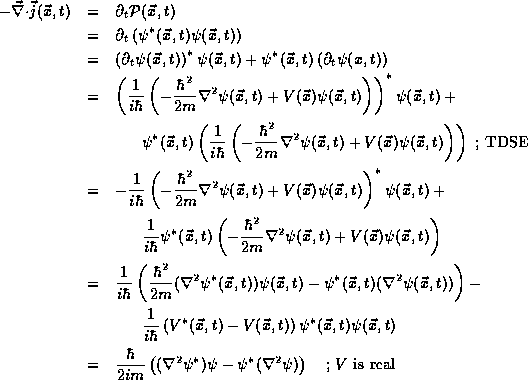
To complete the identification of 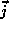 , express the
hand side of the above expression as the divergence of some quantity.
This we do by noting the following identity of vector calculus, which
amounts to integration by parts,
, express the
hand side of the above expression as the divergence of some quantity.
This we do by noting the following identity of vector calculus, which
amounts to integration by parts,
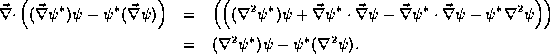
Inserting this into our previous result gives
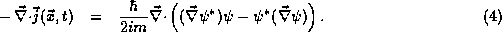
Thus, our final form for the probability current density is
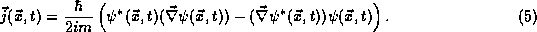
For 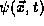 developing under the Schrödinger equation, this
developing under the Schrödinger equation, this
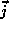 satisfies the continuity equation with no source term,
satisfies the continuity equation with no source term,
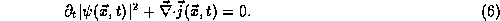
Thus, probability is conserved and the rate of change of probability
in a region V balances the total flux leaving the region,
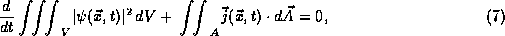
and the total probability in all of space is conserved,
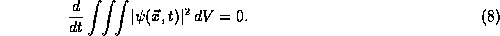
Prof. Tomas Alberto Arias
Thu Oct 12 12:30:23 EDT 1995
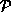 will
remain properly normalized
will
remain properly normalized 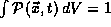 for all time t>0.
The procedure we are about to use is very general. It is used, for
instance, to show that energy and momentum are conserved in
electrodynamics under Maxwell's equations and that mass and momentum
are conserved under the equations of Newtonian fluid flow.
for all time t>0.
The procedure we are about to use is very general. It is used, for
instance, to show that energy and momentum are conserved in
electrodynamics under Maxwell's equations and that mass and momentum
are conserved under the equations of Newtonian fluid flow.
 be conserved is that it obey the
continuity equation with no source term (
be conserved is that it obey the
continuity equation with no source term (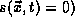 as
as
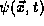 evolves according to the TDSE. To demonstrate
conservation all that we must now do is identify a probability
current density
evolves according to the TDSE. To demonstrate
conservation all that we must now do is identify a probability
current density 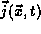 so that
so that 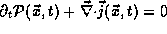 .
.
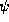 through the TDSE (
through the TDSE (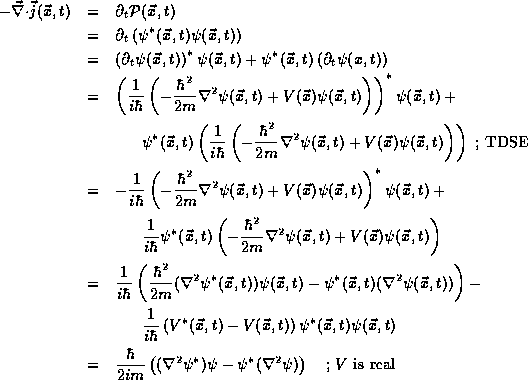
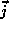 , express the
hand side of the above expression as the divergence of some quantity.
This we do by noting the following identity of vector calculus, which
amounts to integration by parts,
, express the
hand side of the above expression as the divergence of some quantity.
This we do by noting the following identity of vector calculus, which
amounts to integration by parts,
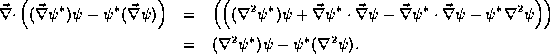
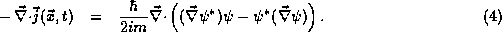
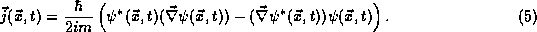
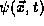 developing under the Schrödinger equation, this
developing under the Schrödinger equation, this
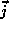 satisfies the continuity equation with no source term,
satisfies the continuity equation with no source term,