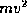 instead of
instead of
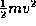 ), then the two constants appearing in the de
Broglie relations would be different, but by precisely the
same factor of one-half.
), then the two constants appearing in the de
Broglie relations would be different, but by precisely the
same factor of one-half.
Note that it is a quite natural consequence of the correspondence
principle that precisely the same constant appears in both the
momentum-wavelength and energy-frequency de Broglie relations
(12). Although these relations related two different
pairs of physical quantities, only one, and not two, fundamental
constants are involved. Ultimately, the equality of these constants
results from our definition of work as force times
distance. If physicists had happened to decide to define work as
one-half times the value of force times distance (so that we could
write the kinetic energy of a particle as 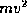 instead of
instead of
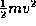 ), then the two constants appearing in the de
Broglie relations would be different, but by precisely the
same factor of one-half.
), then the two constants appearing in the de
Broglie relations would be different, but by precisely the
same factor of one-half.
It is also interesting to ponder the question of why the same value of
Planck's constant should apply for photons as well as for every single
kind of particle. This also comes about as a consequence of
conservation laws. To link the value of Planck's constant for two
different types of particles, we must consider a situation where two
unlike particles interact as for example in the electron-photon
collision in Compton Scattering. A full discussion of how to describe
using waves a system containing more than one particle is beyond the
scope of the course at this stage. We can, however, give a
plausibility argument for the one fact which we need from a more
advanced multiple particle description. To combine the energy of two
particles (say when they are far enough apart that they are no longer
interacting), we know that we simply add the energies of the two
separate particles. As we have just seen, energy and frequency are
related in direct proportion. So, it is plausible that when
combining the waves describing these two particles the frequencies
will add as well. Later we will see how this comes about. For now,
if we accept this idea as plausible, we see that for energy
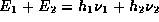 and frequency
and frequency 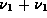 both to
be conserved simultaneously in all collisions exchanging energy/frequency between the
two particles, the particles must share the same value for Planck's
constant
both to
be conserved simultaneously in all collisions exchanging energy/frequency between the
two particles, the particles must share the same value for Planck's
constant 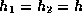 .
.