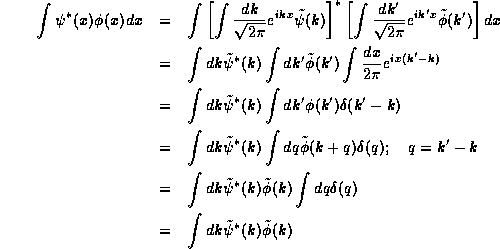You will note that we wrote (14) as an equality rather than as a simple
proportion. This reflects the fact that we have been very careful in
our
choice of constant factors in (12) and (13) so that if
is properly normalized,
So will be 
when computed according to (13)
We will now prove a slightly more general result known as Parseval's Theorem of which this is clearly a special case.
Parseval's Theorem:
To prove this, as with most theorems involving Fourier transforms, we need only use (10.5) and familiar integration techniques.
We proceed as follows:
