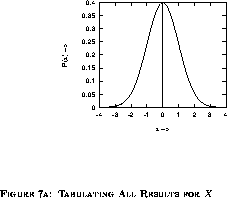
If X and Y are two random variables, we say that they are independent if we get the same distribution for X whether we plot all of our results for X as below,
or whether we plot our results for X when Y falls within a small range of any of its possible values.
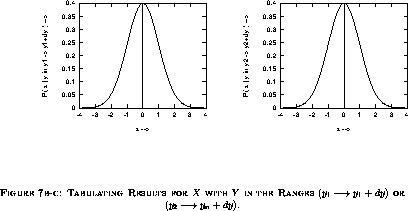
From section (3), we know that the probability that X is
in the range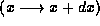 
given that Y is in the range
is just 
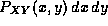. The fact
that all of the distribution curves generated for X, even when Y takes
on different specific values, look precisely the same after proper
normalization by some y-dependent factor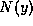 
means that
To find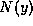 
, we integrate both sides with respect to x,
and so,
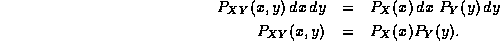
This is the mathematical expression of our physical notion of the independence of experimental variables. If two random variables are independent, then their joint probability distribution is just the product of their individual probability distributions.