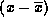 or
or 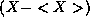 from the average.
But, one then quickly finds
from the average.
But, one then quickly finds
While an experiment may yield well-defined average results, generally every measurement does not yield precisely the same result and there is some spread or variation in the results (as in Figure 3 above). The mathematical concept of variance is an attempt to give a formal measure of this spread.
A first, failed, attempt at defining the variance might be to compute
the average deviation 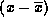 or
or 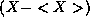 from the average.
But, one then quickly finds
from the average.
But, one then quickly finds
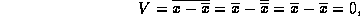
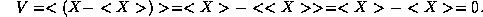
Here we have used the fact that the average value of a constant is just that constant. For instance
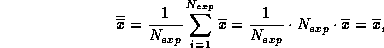
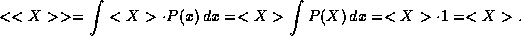
Clearly, this average deviation is not a good measure of the
width of the distribution
in X. The problem is that we get both positive and negative
contributions that then cancel and give us zero. To prevent this from
happening, we can take the average of the square of the
deviation from the average. This is the proper definition of
the variance of X, which is written either as 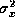 in the
individual measurement picture or as
in the
individual measurement picture or as  in the random
variable picture.
in the random
variable picture.
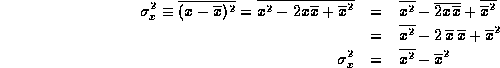
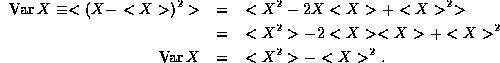
We have used the facts we established in section (3) that the average of a sum is the sum of the averages and that the average of a constant times a random variable is just the constant times the average of the random variable.