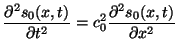Equations of Motion

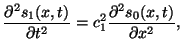As there are no long range forces in this problem, all points interior to each boundary feel forces only from their neighboring points, and so all interior points obey the same equation of motion we have already found for such media, namely the wave equation. Thus, we have

$$\frac{\partial^2 s_0(x,t)}{\partial t^2}=c_0^2 \frac{\partial^2 s_0(x,t)}{\partial x^2}$$ (2)

$$\frac{\partial^2 s_1(x,t)}{\partial t^2}=c_1^2 \frac{\partial^2 s_0(x,t)}{\partial x^2},$$

where $c_0=\sqrt{B_0/\rho_0}$, $c_1=\sqrt{B_1/\rho_1}$.³

The only remaining equation of motion is that for the membrane $x_{\mathrm{mem}}(t)=s_0(x=0,t)=s_1(x=0,t)$. Considering motion only in the x-direction and using the facts that the membrane is massless and that the equilibrium pressures are equal on either side, we find the second boundary condition at $x=0$,

$$m a^{\mathrm{c\,of\,{\bf m}}}_x = \sum F^{\mathrm{(ext)}}_x$$

$$0 \cdot a^{\mathrm{c\,of\,{\bf m}}}_x = +A \left(P_0-B_0 \left.\frac{\partial s_0(x,t)}{\partial x}\right... ...eft(P_1-B_1 \left.\frac{\partial s_1(x,t)}{\partial x}\right\vert _{x=0}\right)$$

$$0 = A \left(-B_0 \left.\frac{\partial s_0(x,t)}{\partial x}\right\ver... ...x=0} + B_1 \left.\frac{\partial s_1(x,t)}{\partial x}\right\vert _{x=0} \right)$$

$$\Rightarrow$$

$$B_0 \left.\frac{\partial s_0(x,t)}{\partial x}\right\vert _{x=0} = B_1 \left.\frac{\partial s_1(x,t)}{\partial x}\right\vert _{x=0}.$$ (3)

We shall refer to this second boundary condition as force balance.⁴