Fixed/Close Boundary Conditions -

These conditions arrise from the type of boundary which we find in Figure 1. In this case, the ends of the string cannot move from the position y=0 without breaking the string. (On the left the string knots around the attaching peg, and on the right the string feeds through the hole.) This type of boundary condition is thus termed a fixed boundary condition. Such a condition is also frequently termed closed because, in the case of sound, a closed end of a pipe prevents motion of the air and creates the same type of fixed boundary condition. Mathematically, a fixed boundary condition leads to the simple condition of zero displacement at the ends of the system,

 

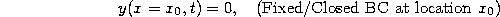
where 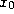gives the location of the fixed boundary ( 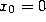or L in Figure 1) and the condition holds for all times t.