Next: Particle in a box Up: Quantum Mechanics Previous: Electron diffraction experiment Contents
From the de Broglie hypothesis, we can quickly predict the outcome of many experiments with elementary particles. The first experiment we shall consider demonstrates something very unusual about elementary particles known as the Heisenberg Uncertainty Principle. This principle what we mean by ``small'' in the idea of the classical limit and is useful in giving quick estimates of quantum mechanical effects.
The basic idea comes from what we already know about the intensity of waves after passing through any opening. The notes on interference show that the intensity of waves passing through a finite slit exhibit the phenomenon of diffraction: no matter how straight the waves approach the opening, on the other side the intensity spreads out over a range of angles. From the de Broglie hypothesis, we expect the same behavior for the probability of finding particles. This has some unusual implications.
Figure 5 shows an experiment where particles of
momentum ![]() are sent directly toward a slit of width
are sent directly toward a slit of width ![]() and
then collected on a observation screen at a large distance
and
then collected on a observation screen at a large distance ![]() from the slit. From the de Broglie hypothesis we have the immediate
result that particles arrive at the screen with all possible random
angles
from the slit. From the de Broglie hypothesis we have the immediate
result that particles arrive at the screen with all possible random
angles ![]() with the same pattern we found for the interference
pattern from a single slit (from LN ``Wave Phenomena II:
Interference'')
with the same pattern we found for the interference
pattern from a single slit (from LN ``Wave Phenomena II:
Interference'')
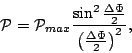 |
(8) |
For this type of experiment, the classical physics prediction is that all
particles should arrive on the screen at the angle ![]() . Consistent
with the concept of the classical limit, this is the most
probable outcome. However, some particles will hit the screen
at almost all angles, with the exception of just a few special points where
the probability just happens to be zero. This means that every time a
baseball is thrown through a door, even in vacuum so that there is nothing
to disturb the path of the ball, there is some chance that it will take a
sharp turn on the other side.
. Consistent
with the concept of the classical limit, this is the most
probable outcome. However, some particles will hit the screen
at almost all angles, with the exception of just a few special points where
the probability just happens to be zero. This means that every time a
baseball is thrown through a door, even in vacuum so that there is nothing
to disturb the path of the ball, there is some chance that it will take a
sharp turn on the other side.
To see how this is not inconsistent with the observations of our daily
lives, it helps to figure out what range of angles are most likely.
The probabilities in Figure 5 tend to be rather
small after the first minima bounding the central maximum. In fact,
over 90% of the area under the curve is contained in the main peak
between these first minima. Thus, with better than 90% certainty, we
can say that the particle will arrive at angles in the range
![]() , so that
, so that
![]() . Using the definitions of
. Using the definitions of ![]() and
and ![]() above, this
gives
above, this
gives
![]() . Thus, the reasonably expected range of
angles is
. Thus, the reasonably expected range of
angles is
Heisenberg realized that this phenomenon of spreading out after being
restricted through an aperture is very general and found a very useful
way of expressing the result in terms of classical concepts about
particles. The slit in Figure 5 restricts the
particles to a range of values ![]() in the
in the ![]() -direction.
The fact that the particles can then be found on the screen at angles
-direction.
The fact that the particles can then be found on the screen at angles
![]() means that after being restricted by the slit in the
means that after being restricted by the slit in the
![]() -direction, the particles now pick up random (!) momenta
-direction, the particles now pick up random (!) momenta ![]() in
the
in
the ![]() -direction of value which the geometry of
Figure 5 determines to be
-direction of value which the geometry of
Figure 5 determines to be
![]() .4 The likely range in these random momenta
is thus
.4 The likely range in these random momenta
is thus
![]() ,
where we have used the likely range of angles from Eq. (9).
Note that this range becomes greater and greater in inverse proportion
as
,
where we have used the likely range of angles from Eq. (9).
Note that this range becomes greater and greater in inverse proportion
as ![]() decreases. Heisenberg described this effect by saying that the
act of constraining a particle to a region of size
decreases. Heisenberg described this effect by saying that the
act of constraining a particle to a region of size ![]() along
the
along
the ![]() -direction results in an uncertainty in its momentum
-direction results in an uncertainty in its momentum ![]() so that
so that
![]() is at least as big as some
constant. (He said ``at least'' as big because it is always possible
to introduce additional sources of uncertainty beyond the fundamental
limit.) In this case, multiplying our results, we find the constant
to turn out to be
is at least as big as some
constant. (He said ``at least'' as big because it is always possible
to introduce additional sources of uncertainty beyond the fundamental
limit.) In this case, multiplying our results, we find the constant
to turn out to be ![]() .
.
A few technical notes are in order. In defining the uncertainty
![]() , we used the range of momenta for which we have 90%
confidence. The precise definition used in advanced courses in
quantum mechanics is to use the standard deviation statistic that we
use in the analysis of exam scores, which gives a somewhat narrower
measure for
, we used the range of momenta for which we have 90%
confidence. The precise definition used in advanced courses in
quantum mechanics is to use the standard deviation statistic that we
use in the analysis of exam scores, which gives a somewhat narrower
measure for ![]() . Also, a ``smoother'' slit where the
particle has some chance of making it through the edges can also
lessen the uncertainty in
. Also, a ``smoother'' slit where the
particle has some chance of making it through the edges can also
lessen the uncertainty in ![]() . Finally, we could just as
easily aligned our slit with the
. Finally, we could just as
easily aligned our slit with the ![]() -axis. When all of this is taken
into account, the precise mathematical statement has been shown to be
that we have separately for each component
-axis. When all of this is taken
into account, the precise mathematical statement has been shown to be
that we have separately for each component ![]() ,
, ![]() and
and ![]() that
that
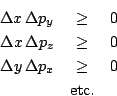
Tomas Arias 2004-11-30