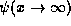To find the allowed energies, we must impose the condition on
(6) that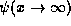 
show no exponentially
growing behavior. To explore the exponential behaviors of the
solution in region III, we expand the hyperbolic functions
in 
in their exponential components,
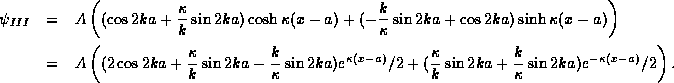
The first term gives rise to exponential growth as
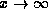and so its prefactor must be zero,
To simplify this condition, we
expand the double angle
trigonometric functions and multiplying through by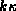 
. (Note that
this may introduce an extraneous root at k=0)
The eigensolution condition
on k and 
then becomes
Having succeeded in factoring our expression in the last step, we have simplified the condition considerably. Unfortunately, the factors still represent fairly complex transcendental equations for the energy E. To proceed, we must resort to a numerical or graphical solution method for each of the two roots of (17).
We will see later that these roots represent either the odd or even solutions, respectively.
The graphical solution proceeds as follows. First we note that k is related to E through (11)
so that working with either k or E is
nearly equivalent. Next, 
and k share the
relationship,
where we have defined
Plotting
the three functions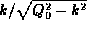 
, 
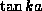and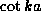 
on the
same graph, the solutions to (18) and (19)
may be read off as the k values of the intersections of the curves
in Figure 1.7.
The first intersection (at k=0) is an extraneous root we introduced
when we multiplied by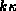 
. This must extraneous root, because
when we let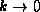 
in (16), which is the value
of the prefactor to the exponentially growing solution in region III,
we get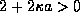 
, which would lead to exponentially growing
solutions. The only extraneous root we introduced was for k=0, all
remaining intersections of the curves in the figure then represent
allowable eigensolultions to the TISE.
From the figure we learn several things. First, we see that there is
always at least one allowed energy, corresponding to the intersection
of the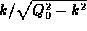 
curve with the first branch of the 
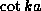curve. This occurs for 
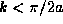and is always the first, lowest
energy (ground state) solution. After that,
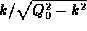heads toward 
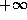at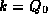 
, and there may
or may not be further solutions according to whether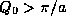 
,
which would
then allow an intersection with the next branch.
For the case in the figure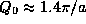 
and so there are three
allowed pure energy states, one at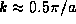 
, 
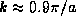and one at 
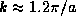. We see that in general there
are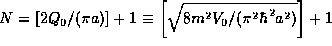 
allowed eigenenergies, where 
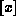is the notation for
taking the integer part of a real number x.
For the
lower bound states, the curve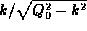 
stays relatively
close to the k-axis so that the solutions are at approximately
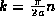for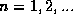 
, correspondingly precisely to the
Bohr-Sommerfeld solutions
for a particle in a box of size
2a and matching, as we shall discuss shortly, the eigenenergies for
the infinite square well,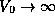 
. This is physically
reasonable, if the solutions have energies E far below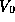 
, these
states act as through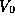 
were infinite.
Finally, note that as E (or equivalently k) increases the
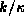curve intersects alternately the two curves 
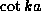and
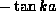so that the 
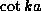root corresponds to even numbered
excited solutions (we regard the ground state as n=0)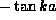 
root corresponds to the odd numbered solutions.
