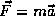Massachusetts Institute of Technology
Department of Physics
Physics 8.04 Thu Oct 12 21:20:54 EDT 1995
In the course, we have established so far all that is needed in
principle to predict quantum phenomena. We have a theory of operators and
averages which tells us how to predict the statistical outcome of
experiments given the wavefunction describing a system at the time the
experiments are performed. To tell us the dynamics of quantum states
we have the
the time dependent Schrödinger equation (TDSE) to tell us how the
wavefunction of a system evolves in time. We have even shown to prove
Newton's equation of motion,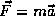 
as a consequence of our
quantum dynamics.
The next phase of the scientific program is to predict new phenomena using the quantum theory. In order to do this, we developed the method of separation of variables and found a complete, albeit formal, solution of the TDSE:
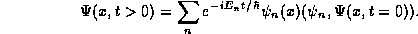
This ``complete'' solution to the TDSE, however, is written
in terms of the solutions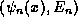 
of yet another equation,
the time independent
Schrödinger equation (TISE):
The final link which will allow us to predicting quantum phenomena is to learn how to solve this final equation, the TISE.
Learning this is best done by working through examples in detail. We shall begin in Section 1 with the solution of the TISE in finite square well. We will begin with one of the more complicated examples because by working with it, we will touch on most of the issues faced in the solution of the TISE.
In a later set of notes, we will discuss the solution of two special limiting cases of the finite square well, the infinite square well and the attractive delta potential. We will show how the solutions for these systems may be obtained either through taking the appropriate limit of our solutions to the finite square well or by solving the TISE in these potentials directly.
