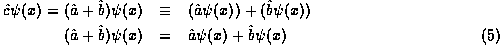
and 
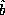, we may define a third
operator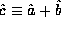 
, the operator sum of 
and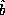 
, whose operation is defined as applying 
and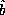 
separately and then summing the results,
Note that, this definition is the same a saying that operator addition exhibits the usual algebraic distributive property when acting on functions to the right. From the definition of the operator sum and the usual associative property of addition, we may show that function operator addition is itself associative,
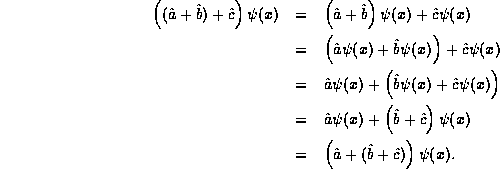
Since the result of the operation of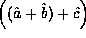 
and
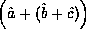is the same on all functions 
,
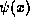these two operators must be equal,
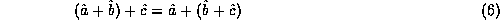
Similarly, one may show that operator addition is commutative,
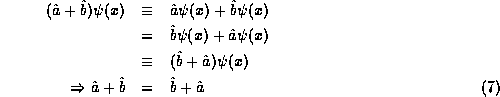
Finally, the zero operator mentioned in the previous subsection is the
additive identity. (One may easily show following the same procedure
as in the proofs above that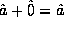 
.) With an additive
identity, subtraction of function operators may be defined in the
familiar way.
