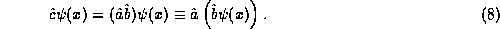
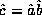of two operators to be
the result of their sequential application,
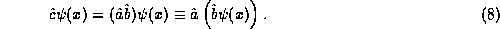
This procedure is sensible since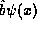 
returns a new
function which may then be fed to 
as input to produce the final
output defined as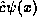 
.
Like the familiar multiplication of numbers, the function operator
product is also associative, as we see by studying the action of a
three-way product on an arbitrary function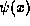 
,
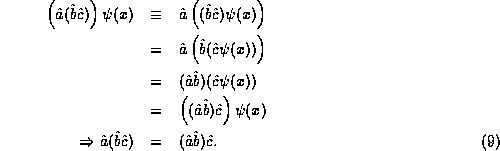
As the operator product is associative, without ambiguity we may write
the product
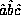without parenthesis. As with normal
multiplication, raising an operator to an integer power is just a
short-hand for repeated application of the operator,
Note that in our notation there is a subtle difference between
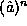and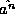 
. The former is the product of n factors
of 
as defined in (10) above, while the later is a
single operator, defined physically so that the quantum average
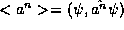is given correctly. Although,
they will turn out to be equal, the definitions of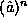 
and
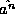are entirely different.
There is one key property which our operator product does not share
with common multiplication. Defined as the sequential
application of two operations, there is no reason to expect that the
operator product be commutative, that the net affect of two operations
be independent of the sequence in which they are applied.
Symbolically, we expect in general that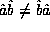 
. This
property of operators is closely related to the Heisenberg uncertainty
principle. The drive to give this basic principle of quantum physics
a direct expression in our mathematical formalism is a key force in
our choice of the definition of operator product in terms of
sequential application. Because of the prime importance of the
non-commutivity of the operator product, we will dedicate the entire next
section to the issue of commutivity.
Before discussing non-commutivity, there are two final properties of
the operator product which mimic normal multiplication and with which
the student should be familiar. First, as with common multiplication,
there is an operator multiplicative identity. It is just the constant
operator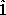 
discussed in the previous subsection. It is easily
verified, using the procedures above that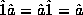 
. (Note that one must consider both a left and a right identity
as the operator product is not commutative.) One may also show that
multiplication by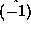 
yields the additive inverse of an
operator, (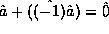
.
The final familiar property of the operator product is the distributive property,
The ``commuted'' form of this statement,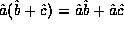 
,
does not follow directly. While true for quantum operators, it is not
true for general operators and
depends on a property known as linearity which we shall discuss
in detail in section (4.1).
