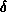Using the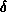 
-function we may now complete the integral in (10),
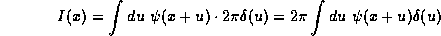
The integral appears as the product of the two functions in Figure 3.4.2.
Because the peak may be made arbitrarily narrow, the values of u which
contribute to the integral are so tiny that we may make the
approximation
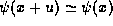with a small error proportional to at
most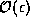 
and which will vanish in the final limit
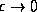. Thus, we have
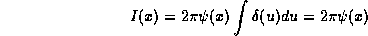
Our initial guess was nearly correct! We have found
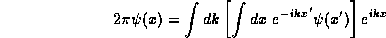
or
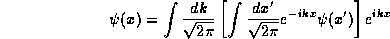
This tells us that if we take the superposition
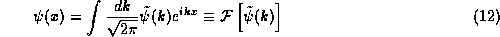
we may find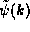 
from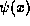 
from the inverse
relationship
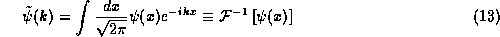
(12) and (13) taken together are the Fourier inversion theorem, where
the operation in (12),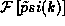 
is known
as the Fourier transform, while the operation in (13),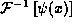 
is the inverse Fourier transform.
