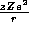In the notation of problem 1.5 from the first problem set, classical
analysis gives the differential scattering cross section for a
repulsive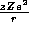 
Coulomb potential to be
where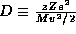 
is the distance of closest
possible approach of an alpha particle of charge ze=2e, mass M and
traveling at velocity v to a heavy nucleus of charge Ze. Note
that, unlike the case of scattering from hard spheres, the cross
section depends on both the velocity of the incoming particles and the
scattering angle. Using the same approach as in the solutions to
problem 1.5, answer the following two questions:
a) A beam of 
-particles, of kinetic energy 5 MeV and
intensity 
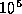particle/sec, is incident normally on a gold foil of
thickness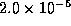 
cm. (The density, atomic weight and
atomic number of gold are 19.3 g/cm
, 197 and 79 respectively.)
An 
particle counter of area 0.25 cm
is placed on the
opposite side of the foil from the incoming beam at a distance
of 100 cm at an angle of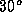 
from the incoming flux. How many
counts should we expect per hour if the detector registers all
particles passing through it? How many counts will there be per hour
for back-scattering events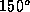 
away from the direction of
incoming flux?
b) The density and atomic weight of copper are 8.9 g/cm
and 63.6,
respectively. If Rutherford scattering through a copper foil of
thickness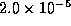 
cm at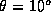 
using the same
detector and 
-particle source as in (a) gives 46 counts per
hour, what then do you deduce for the charge on the copper nucleus?