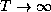Consider a three-state system as indicated in the diagram in Figure 2. Here the first two states, 1 and 2, have the same energy. (This situation is referred to as a ``degeneracy''.)
a) What do you expect the average energy of this system to be at
absolute zero temperature (T=0)? At extremely high temperatures
(
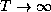)? Why?
b) To confirm your expectations, apply the Boltzmann distribution to
write the probability of each of the three states as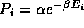 
, where 
is the proportionality constant and
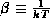, where k is Boltzmann's constant. Use
the condition that these probabilities must sum to unity (the
normalization of the probability distribution) to determine
. Finally, compute the average energy of this system at
temperature T and verify your predictions in a) for the
behavior of this system as 
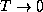and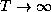 
.
c) Confirm that the shortcut of summing the partition
function,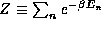 
, and then taking
gives the correct result.
