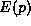 and wave-packets
propagating under a dispersion relation given by
and wave-packets
propagating under a dispersion relation given by 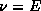 ,
,
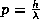 . In this problem you will consider the same
correspondence but for a particle in a system with potential energy.
. In this problem you will consider the same
correspondence but for a particle in a system with potential energy.
In lecture, we considered the correspondence between particles moving
in free space according to an energy function 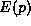 and wave-packets
propagating under a dispersion relation given by
and wave-packets
propagating under a dispersion relation given by 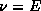 ,
,
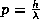 . In this problem you will consider the same
correspondence but for a particle in a system with potential energy.
. In this problem you will consider the same
correspondence but for a particle in a system with potential energy.
Consider a particle whose energy is given by

Written this way, as a function of the momentum p, the energy function of the particle has a special name. It is known as the ``Hamiltonian,'' and so we call the energy here ``H'' instead of the more familiar ``E''.
Imagine that an external force 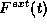 is applied to this
particle in this system in such a way that the momentum of the
particle as a function of time is given by
is applied to this
particle in this system in such a way that the momentum of the
particle as a function of time is given by 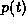 .
.
a) Use conservation of momentum to determine
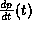 in terms of the force acting on the particle
in terms of the force acting on the particle
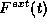 , the position of the particle
, the position of the particle 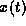 and the potential
function
and the potential
function 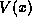 .
.
b) Use conservation of energy to balance the change in energy
H of the particle against the rate at which the external force does
work 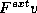 , where
, where 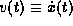 .
Show that
.
Show that
Is this relation true even when the external force is zero?
c) Show that when the external force is zero we also have,
Eq. (2) and Eq. (3) taken together are known as the canonical equations of Hamilton, and are studied in detail in 8.06.
d) Now consider a wave-packet description of the same particle.
So long as the wavelength of the waves are much smaller than the
scales over which 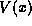 varies, we can imagine a very localized
wave-packet in place of our particle. Around each location in space
x where the packet can be centered, there is then a different
local dispersion relation
varies, we can imagine a very localized
wave-packet in place of our particle. Around each location in space
x where the packet can be centered, there is then a different
local dispersion relation 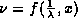 . Given f,
what velocity we would associate with a wave-packet centered about
wavelength
. Given f,
what velocity we would associate with a wave-packet centered about
wavelength 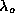 and position
and position 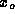 ?
?
e) For motion of the particle in the wave-packet description to
be consistent with the motion determined in the particle description
(Eq.'s (2-3)), what must be the form for
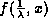 in terms of
in terms of 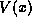 and
and 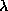 ?
Show that we have again the same correspondence as in
class,
?
Show that we have again the same correspondence as in
class, 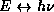 and
and 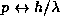 .
.
f) What local dispersion relation would you need to make a wave-packet oscillate back and forth in simple harmonic motion? (See Figure 2.)