


Next: a)
Up: No Title
Previous: e)
A particle of mass m moves though a viscous medium. (See Figure
4.) In this medium, if the particle moves with a velocity
v, it experiences a drag force  given by
given by  .
.
 is known as the relaxation time. If a particle moves through
this medium without an external driving force, its velocity will decay
exponentially to zero with a characteristic time
is known as the relaxation time. If a particle moves through
this medium without an external driving force, its velocity will decay
exponentially to zero with a characteristic time  according to
according to
 . Essentially, the particle ``forgets'' what
it had been doing more that a few relaxation times in the past.
. Essentially, the particle ``forgets'' what
it had been doing more that a few relaxation times in the past.
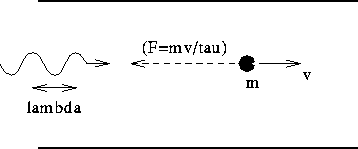
In this problem, the particle is illuminated from the left and absorbs
photons of wavelength 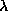 at an average rate of I photons per unit
time. As a result, the particle
experiences an average force and is driven to the right at an average
velocity <v>. Because the photons arrive randomly as discrete
packets, the velocity of the particle is not steady and fluctuates
about the average with fluctuations of typical size
at an average rate of I photons per unit
time. As a result, the particle
experiences an average force and is driven to the right at an average
velocity <v>. Because the photons arrive randomly as discrete
packets, the velocity of the particle is not steady and fluctuates
about the average with fluctuations of typical size  . Your
task is to compute <v> and
. Your
task is to compute <v> and  .
.
Prof. Tomas Alberto Arias
Thu Oct 12 19:22:57 EDT 1995
 given by
given by  .
.
 is known as the relaxation time. If a particle moves through
this medium without an external driving force, its velocity will decay
exponentially to zero with a characteristic time
is known as the relaxation time. If a particle moves through
this medium without an external driving force, its velocity will decay
exponentially to zero with a characteristic time  according to
according to
 . Essentially, the particle ``forgets'' what
it had been doing more that a few relaxation times in the past.
. Essentially, the particle ``forgets'' what
it had been doing more that a few relaxation times in the past.
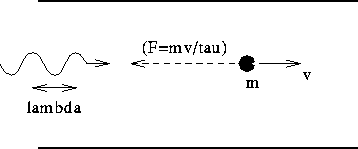
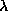 at an average rate of I photons per unit
time. As a result, the particle
experiences an average force and is driven to the right at an average
velocity <v>. Because the photons arrive randomly as discrete
packets, the velocity of the particle is not steady and fluctuates
about the average with fluctuations of typical size
at an average rate of I photons per unit
time. As a result, the particle
experiences an average force and is driven to the right at an average
velocity <v>. Because the photons arrive randomly as discrete
packets, the velocity of the particle is not steady and fluctuates
about the average with fluctuations of typical size  . Your
task is to compute <v> and
. Your
task is to compute <v> and  .
.