


Next: Scattering states
Up: No Title
Previous: Generating wavefunctions
Background: This problem set contains only three problems.
Problems 3 and 4 from this problem set are actually a single problem
broken into two parts for grading purposes.
In this problem you will consider particles of mass m in a quantum
state approaching, from the left hand side, a potential barrier of
height  and length L. See Figure 1. The state
of the particles is that of a Gaussian probability distribution with
momentum centered about kinetic energy
and length L. See Figure 1. The state
of the particles is that of a Gaussian probability distribution with
momentum centered about kinetic energy 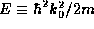 .
Although classically, the particles do not have enough energy to
enter the barrier region 0<x<L, quantum mechanically there is
a non-zero probability that the particles will appear on the other
side of the barrier. This phenomenon is referred to as ``quantum
tunneling''. In this problem you will consider not only the
probability of an event of quantum tunneling, but also consider such
issues as the time spent inside the forbidden region (often thought to
be zero in science fiction stories and thus allowing faster than light
travel!) and the effects of the tunneling process on the wave packet
emerging on the other side.
.
Although classically, the particles do not have enough energy to
enter the barrier region 0<x<L, quantum mechanically there is
a non-zero probability that the particles will appear on the other
side of the barrier. This phenomenon is referred to as ``quantum
tunneling''. In this problem you will consider not only the
probability of an event of quantum tunneling, but also consider such
issues as the time spent inside the forbidden region (often thought to
be zero in science fiction stories and thus allowing faster than light
travel!) and the effects of the tunneling process on the wave packet
emerging on the other side.

Figure 1: Quantum tunneling problem
Prof. Tomas Alberto Arias
Tue Apr 30 08:11:46 EDT 1996
 and length L. See Figure 1. The state
of the particles is that of a Gaussian probability distribution with
momentum centered about kinetic energy
and length L. See Figure 1. The state
of the particles is that of a Gaussian probability distribution with
momentum centered about kinetic energy 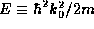 .
Although classically, the particles do not have enough energy to
enter the barrier region 0<x<L, quantum mechanically there is
a non-zero probability that the particles will appear on the other
side of the barrier. This phenomenon is referred to as ``quantum
tunneling''. In this problem you will consider not only the
probability of an event of quantum tunneling, but also consider such
issues as the time spent inside the forbidden region (often thought to
be zero in science fiction stories and thus allowing faster than light
travel!) and the effects of the tunneling process on the wave packet
emerging on the other side.
.
Although classically, the particles do not have enough energy to
enter the barrier region 0<x<L, quantum mechanically there is
a non-zero probability that the particles will appear on the other
side of the barrier. This phenomenon is referred to as ``quantum
tunneling''. In this problem you will consider not only the
probability of an event of quantum tunneling, but also consider such
issues as the time spent inside the forbidden region (often thought to
be zero in science fiction stories and thus allowing faster than light
travel!) and the effects of the tunneling process on the wave packet
emerging on the other side.
