In lecture, we considered the correspondence between particles moving
in free space according to an energy function E(p) and wave-packets
propagating under a dispersion relation given by 
and
. In this problem you will consider the same
correspondence but for a particle in a system with potential energy.
Consider a particle whose energy is given by
Written this way, as a function of the momentum p, the energy function of the particle has a special name. It is known as the ``Hamiltonian,'' and so we call the energy here ``H'' instead of the more familiar ``E''.
Imagine that an external force 
is applied to the
particle in this system in such a way that the momentum of the
particle as a function of time is given by p(t).
a) Determine 
in terms of the force
acting on the particle , the position of the particle
x(t) and a derivative of the potential function V(x). (Note that
this amounts to applying the concept of conservation of momentum.)
b) (briefly) why 
.
Thus, show that
Is this relation true even when the external force is zero?
c) Show that when the external force is zero we also have
Eq. (2) and Eq. (3) taken together are known as the canonical equations of Hamilton, which you studied in detail in 8.033/8.21.
d) Now consider a wave-packet description of the same particle.
If the wavelength of the waves are much smaller than the scales over
which V(x) varies, near each point 
in space, waves of a given
frequency 
, will appear with nearly constant wave lengths so
that we may define for these waves a local wave number
, which will depend on the region of space at
which we are making the observations and the frequency of the wave.
(Note that the function may be inverted for each
to find a local (spatially dependent) version of the
usual dispersion relation, 
.
Using the method of stationary phase, , in terms
of 
, the velocity of
the following wave packet
for points x near . ( 
is sharply peaked near a
frequency 
such that 
.)
e) For motion of the particle in the wave-packet description to
be consistent with the motion determined in the particle description
(Eq. (2)), what must be the form for
in terms of V(x) and k, if we accept the
identification 
?
Show again that we must therefore have the same correspondence as in
class, 
.
f) Figure 1 shows the path of an electron
passing though JJ Thomson's apparatus with the electric field turned
off and the magnetic field turned on. What local dispersion relation
for waves between the plates would be needed to
make a wave-packet follow the same trajectory? (Be sure to
this one over with your recitation instructor if you do not
understand what this problem is getting at.)
Hints:
The energy of an electron in the constant magnetic field B shown in the picture is
and the Hamiltonian for an electron in the same magnetic field is
where
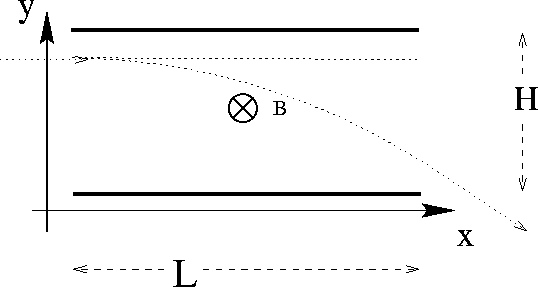
Figure 1: Electron moving through a magnetic field
