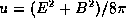 .
.
Here we imagine that the states available to the system are described
by a continuous range of possibilities. In this case, we consider a
single electromagnetic mode which can contain any amount of energy.
Now we may expect all combinations of values for the strengths of the
electric E and magnetic B fields, and the energy of the
electromagnetic mode is 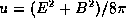 .
.
Because the allowed states are described by any values for E and B, to get the partition function in analogy with Eq. (7) we integrate instead of sum:
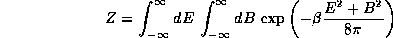
To evaluate this integral, we can change variables to polar
coordinates 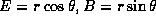 , where
, where 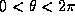 and
and 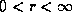 . After this, we make a
second change of variables to
. After this, we make a
second change of variables to 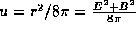 and
render the result in a simple form:
and
render the result in a simple form:
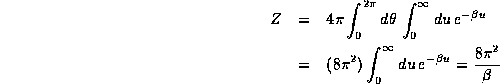
So, then, in this case
This result doesn't match the experimental 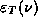 either, but this result gives the correct result
for small
either, but this result gives the correct result
for small  .
.