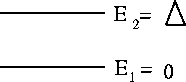
Image the two-level system in the figure below:
Taking the constant of proportionality to be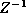 
, the Boltzmann
distribution gives for the probability of being in the states 1 or 2
at temperature T,
The normalization condition that the probabilities must sum to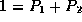 
then determines the normalization constant Z to be
Here we have also written Z, known as the Partition Function, in a form also for valid for a general system. In the most general case, Z is just the sum of the Boltzmann factor over all states available to the system. In this case it happens that n takes just the values 1 and 2.
Next the average energy is
which we found we could write in the convenient form
where Z is given as in Eq. (7).
The specific results for the two-level system are then just
and
Note that <E> has the expected property that 
as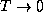 
, and the counter-intuitive but reasonable property that
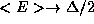as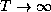 
.
Also note, that as a function of 
, <E> decays like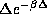 
for large 
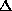, reminiscent of the
decay in the experimental 
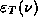for
large 
.
