


Next: The Classical Limit
Up: Application to a
Previous: Application to a
If we have a particle of mass M confined to a box of length L
centered on the origin x=0, then repeated simultaneous measurements
of the position X and momentum P of the particle will yield
distributions about some mean values <X> and <P> with
characteristic widths 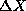 and
and 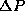 , respectively. In this
case, <X> will be centered somewhere within the confines of the box
and the width of this distribution in X will have a width no greater
than
, respectively. In this
case, <X> will be centered somewhere within the confines of the box
and the width of this distribution in X will have a width no greater
than 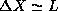 . Additionally, we expect from symmetry that
the distribution in momenta which we measure will also be centered
about <P>=0, and by the Uncertainty Principle, we know that there
will be some width in the momentum distribution
. Additionally, we expect from symmetry that
the distribution in momenta which we measure will also be centered
about <P>=0, and by the Uncertainty Principle, we know that there
will be some width in the momentum distribution 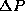 as well.
as well.
Now, technically, if we knew that that the distribution within the box
were uniform, we could use the precise result from the lecture notes
on statistics that 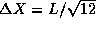 . However, at this point we
know very little about the shape of the probability distribution
(later in the course we will see explicitly that this distribution is
not uniform. One could argue that, still
. However, at this point we
know very little about the shape of the probability distribution
(later in the course we will see explicitly that this distribution is
not uniform. One could argue that, still 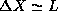 is
likely an overestimate. While this may be true, we will not concern
ourselves with such precise factors here because we know that in the end, the
results we generate at this point are just estimates of orders of
magnitude.
is
likely an overestimate. While this may be true, we will not concern
ourselves with such precise factors here because we know that in the end, the
results we generate at this point are just estimates of orders of
magnitude.
With all this in mind, it is safe to say that 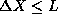 .
The uncertainty principle states, however, that
.
The uncertainty principle states, however, that 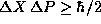 . Thus we conclude that
. Thus we conclude that 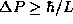 .
Here again, we are being sloppy with the factor of two. We really
don't trust our result to more than an order of magnitude, and so there
no point carrying extra factors which take time to write down and
to track. For instance, we could just as well write
.
Here again, we are being sloppy with the factor of two. We really
don't trust our result to more than an order of magnitude, and so there
no point carrying extra factors which take time to write down and
to track. For instance, we could just as well write 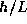 instead of
instead of
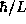 . At this level of analysis either starting point will lead
to equally valid results.
. At this level of analysis either starting point will lead
to equally valid results.
If we now ask for the kinetic energy of the particle

it too will have some distribution. On average,

and now we need to estimate 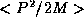 . P
typically has values in the range
. P
typically has values in the range 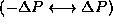 and so in order of magnitude, typically,
and so in order of magnitude, typically, 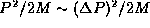 and so
and so 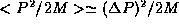 . This rough physical argument is
all that is required in this discussion. If, however, you are
uncomfortable with this, you can also use the precise statistical
definition of
. This rough physical argument is
all that is required in this discussion. If, however, you are
uncomfortable with this, you can also use the precise statistical
definition of 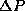 from the supplemental notes on statistics,
from the supplemental notes on statistics, 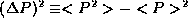 . Combining this with the fact that <P>=0,
precisely
. Combining this with the fact that <P>=0,
precisely 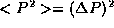 . Using either argument, we have
. Using either argument, we have

There is thus an absolute minimum average energy which are particle
may have,

(Again, there is no point in tracking the factor of two which we have dropped.)
To get a feel for the importance of this result, we note that for an
electron 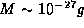 confined inside of an atom
confined inside of an atom 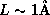 ,
, 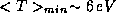 , which is nearly half of the binding energy of hydrogen
and thus the energy of confinement is a significant and important
effect in chemistry and atomic physics. The electron has a non-zero
kinetic energy, just by virtue of its confinement to a finite region
of space. This very general principle follows directly from the
uncertainty principle, and just as the uncertainty principle holds
regardless of the physical situation or apparatus, we will see that
the energy of confinement arises in all situations regardless of the
agent which causes the confinement. The confinement may arise
explicitly from the presence of a rigid box or come about from the
attractive interaction between of the electron to a particular region
of space (to the vicinity of the proton in an atom, for instance).
, which is nearly half of the binding energy of hydrogen
and thus the energy of confinement is a significant and important
effect in chemistry and atomic physics. The electron has a non-zero
kinetic energy, just by virtue of its confinement to a finite region
of space. This very general principle follows directly from the
uncertainty principle, and just as the uncertainty principle holds
regardless of the physical situation or apparatus, we will see that
the energy of confinement arises in all situations regardless of the
agent which causes the confinement. The confinement may arise
explicitly from the presence of a rigid box or come about from the
attractive interaction between of the electron to a particular region
of space (to the vicinity of the proton in an atom, for instance).



Next: The Classical Limit
Up: Application to a
Previous: Application to a
Prof. Tomas Alberto Arias
Wed Oct 11 20:36:54 EDT 1995
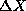 and
and 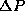 , respectively. In this
case, <X> will be centered somewhere within the confines of the box
and the width of this distribution in X will have a width no greater
than
, respectively. In this
case, <X> will be centered somewhere within the confines of the box
and the width of this distribution in X will have a width no greater
than 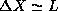 . Additionally, we expect from symmetry that
the distribution in momenta which we measure will also be centered
about <P>=0, and by the Uncertainty Principle, we know that there
will be some width in the momentum distribution
. Additionally, we expect from symmetry that
the distribution in momenta which we measure will also be centered
about <P>=0, and by the Uncertainty Principle, we know that there
will be some width in the momentum distribution 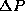 as well.
as well.
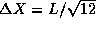 . However, at this point we
know very little about the shape of the probability distribution
(later in the course we will see explicitly that this distribution is
not uniform. One could argue that, still
. However, at this point we
know very little about the shape of the probability distribution
(later in the course we will see explicitly that this distribution is
not uniform. One could argue that, still 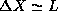 is
likely an overestimate. While this may be true, we will not concern
ourselves with such precise factors here because we know that in the end, the
results we generate at this point are just estimates of orders of
magnitude.
is
likely an overestimate. While this may be true, we will not concern
ourselves with such precise factors here because we know that in the end, the
results we generate at this point are just estimates of orders of
magnitude.
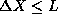 .
The uncertainty principle states, however, that
.
The uncertainty principle states, however, that 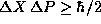 . Thus we conclude that
. Thus we conclude that 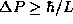 .
Here again, we are being sloppy with the factor of two. We really
don't trust our result to more than an order of magnitude, and so there
no point carrying extra factors which take time to write down and
to track. For instance, we could just as well write
.
Here again, we are being sloppy with the factor of two. We really
don't trust our result to more than an order of magnitude, and so there
no point carrying extra factors which take time to write down and
to track. For instance, we could just as well write 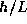 instead of
instead of
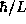 . At this level of analysis either starting point will lead
to equally valid results.
. At this level of analysis either starting point will lead
to equally valid results.


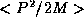 . P
typically has values in the range
. P
typically has values in the range 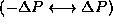 and so in order of magnitude, typically,
and so in order of magnitude, typically, 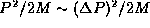 and so
and so 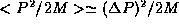 . This rough physical argument is
all that is required in this discussion. If, however, you are
uncomfortable with this, you can also use the precise statistical
definition of
. This rough physical argument is
all that is required in this discussion. If, however, you are
uncomfortable with this, you can also use the precise statistical
definition of 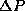 from the supplemental notes on statistics,
from the supplemental notes on statistics, 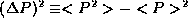 . Combining this with the fact that <P>=0,
precisely
. Combining this with the fact that <P>=0,
precisely 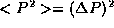 . Using either argument, we have
. Using either argument, we have


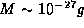 confined inside of an atom
confined inside of an atom 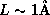 ,
, 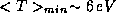 , which is nearly half of the binding energy of hydrogen
and thus the energy of confinement is a significant and important
effect in chemistry and atomic physics. The electron has a non-zero
kinetic energy, just by virtue of its confinement to a finite region
of space. This very general principle follows directly from the
uncertainty principle, and just as the uncertainty principle holds
regardless of the physical situation or apparatus, we will see that
the energy of confinement arises in all situations regardless of the
agent which causes the confinement. The confinement may arise
explicitly from the presence of a rigid box or come about from the
attractive interaction between of the electron to a particular region
of space (to the vicinity of the proton in an atom, for instance).
, which is nearly half of the binding energy of hydrogen
and thus the energy of confinement is a significant and important
effect in chemistry and atomic physics. The electron has a non-zero
kinetic energy, just by virtue of its confinement to a finite region
of space. This very general principle follows directly from the
uncertainty principle, and just as the uncertainty principle holds
regardless of the physical situation or apparatus, we will see that
the energy of confinement arises in all situations regardless of the
agent which causes the confinement. The confinement may arise
explicitly from the presence of a rigid box or come about from the
attractive interaction between of the electron to a particular region
of space (to the vicinity of the proton in an atom, for instance).