


Next: About this document
Up: No Title
Previous: Ground State/Zero Point
Finally, we consider a system of Hydrogen atoms which have been left
alone to radiate all of their excess energy. Classically, we would
eventually (after about 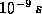 ) expect to find that all of the
electrons have fallen into the nuclei at R=0. According to the
uncertainty principle, however, there must remain an uncertainty in
the position
) expect to find that all of the
electrons have fallen into the nuclei at R=0. According to the
uncertainty principle, however, there must remain an uncertainty in
the position 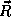 (measured from the proton) and momentum
(measured from the proton) and momentum 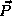 of the electrons. Again, we expect
of the electrons. Again, we expect 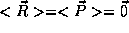 . But
that there will be some spread
. But
that there will be some spread 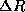 and
and  in the
distributions.
in the
distributions.
In a hydrogen atom the energy of the electron is given by

where M and e are the charge and mass of the electron respectively.
The average energy we expect for our system of hydrogen atoms is then

Here, as with the box, we are again being sloppy with precise values
and are just making an order of magnitude estimate in order to gain
qualitative understanding of the physics of the hydrogen atom.
We now apply the uncertainty principle, which tells us that  so that
so that
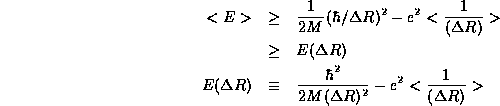
Once again, we find a lower bound on <E> by finding the minimum of
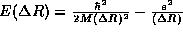 . Setting the derivative equal to zero,
. Setting the derivative equal to zero,

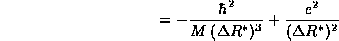
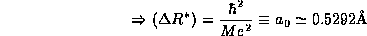
The value we find for the width of the distribution of the electron
about the proton is precisely the experimental size of the Hydrogen atom! The
combination of constants which given this distance, 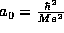 , appears so often in atomic physics that is given
a special name, the Bohr radius.
, appears so often in atomic physics that is given
a special name, the Bohr radius.
Finally, we have our estimate of the average energy of our systems in
their ground state,

which happens to be precisely the ionization energy of Hydrogen,
the energy it takes to remove an electron from a hydrogen atom when it
is in its ground state!
The exact agreement is accidental because this is only a
semiquantitative argument. The fact that we got the correct order of
magnitude is not an accident. It is a consequence of the fact that
our argument contains all of the correct physics in this situations.
Note also the from this argument alone, we cannot understand why it is
that all hydrogen atoms in their ground state have precisely the same
ionization energy. This argument merely puts a limit on the lower
bound the average ionization energy may have. There is no problem if
all hydrogen atoms require the same energy for ionization, so long at
that energy does not violate (4). The equality of the
ionization energies for all hydrogen atoms in the ground state is an
indication that there are strong correlations in the
distributions for R and P. (See the notes on statistics for a
discussion of correlation).
Finally, our results are in accord with the classical limit. As
 we find
we find 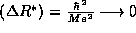 and
and 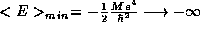 ; the electron ``falls'' into the infinite
well of the proton as expected classically.
; the electron ``falls'' into the infinite
well of the proton as expected classically.



Next: About this document
Up: No Title
Previous: Ground State/Zero Point
Prof. Tomas Alberto Arias
Wed Oct 11 20:36:54 EDT 1995
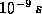 ) expect to find that all of the
electrons have fallen into the nuclei at R=0. According to the
uncertainty principle, however, there must remain an uncertainty in
the position
) expect to find that all of the
electrons have fallen into the nuclei at R=0. According to the
uncertainty principle, however, there must remain an uncertainty in
the position 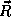 (measured from the proton) and momentum
(measured from the proton) and momentum 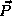 of the electrons. Again, we expect
of the electrons. Again, we expect 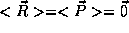 . But
that there will be some spread
. But
that there will be some spread 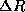 and
and  in the
distributions.
in the
distributions.


 so that
so that
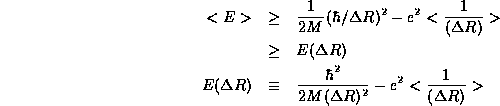
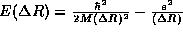 . Setting the derivative equal to zero,
. Setting the derivative equal to zero,

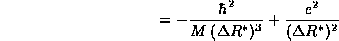
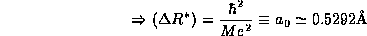
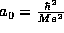 , appears so often in atomic physics that is given
a special name, the Bohr radius.
, appears so often in atomic physics that is given
a special name, the Bohr radius.

 we find
we find 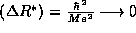 and
and 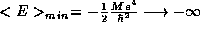 ; the electron ``falls'' into the infinite
well of the proton as expected classically.
; the electron ``falls'' into the infinite
well of the proton as expected classically.