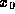 ,
,
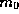 and
and 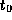 , respectively, we have the conversions
, respectively, we have the conversions 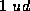 =
= 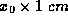 ,
, 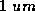 =
=  , and
, and 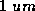 =
= 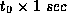 .
.
In the cgs system of units we have been using throughout this course, there are just three fundamental dimensions, or types of physical quantities: distance L (measured in units of cm), mass M (measured in units of gm) and time T (measures in units of sec). Dimension refers to the type of physical quantity being measured (distance, mass, time) and unit refers to the amount of that quantity which we agree to call one one unit (1 cm, 1 gm, 1 sec). Note that the cgs system has no basic dimension of charge because the cgs unit of charge is defined as the amount of charge needed to produce a unit force between two objects at a unit distance and thus requires the introduction of no additional dimension. The unit of charge in this system (the esu), on the other hand, does scale with the units of the fundamental dimensions; if we changed the unit of distance then the amount of charge required to produce a unit force at a unit distance would change.
The fundamental cgs units of 1 cm, 1 gm, and 1 sec were
chosen for historical reasons; we can we can imagine
different worlds in which all of the formulas of physics are the same
but where the numerical values which we insert for the experimental
constants in our equations are different. Rather than accept these
historical dimensional units, we can take a more active role and make
our own judicious choice of units for each problem at hand, picking
our own most convenient unit distance, mass and time. For the
purposed of this discussion we will name them 1 ud, 1 um and 1
ut respectively, for one ``unit distance,'' one ``unit mass,'' and
one ``unit time,'' respectively. These new units correspond to some
amount of the standard cgs units. Calling these amounts 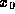 ,
,
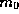 and
and 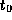 , respectively, we have the conversions
, respectively, we have the conversions 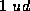 =
= 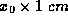 ,
, 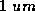 =
=  , and
, and 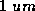 =
= 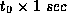 .
.
Having moved to different units for the fundamental dimensions of
length, mass and time, will we also have different units for all
compound, or derived, dimensions such as force ( mass
times length times time ) or energy (
mass times length
) or energy (
mass times length times time
times time ). We arrive
at the units of these physical quantities through the familiar
procedure of changing units. A table of examples of the conversion
procedure for the basic dimensions and some dimensions of other common
physical quantities is given in the table below.
). We arrive
at the units of these physical quantities through the familiar
procedure of changing units. A table of examples of the conversion
procedure for the basic dimensions and some dimensions of other common
physical quantities is given in the table below.
