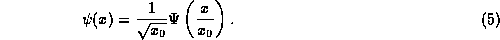Next: Self-trasnform property of
Up: Dimensional Analysis
Previous: Motivation and General
Rather than working in units where mass in measured in gm, the most
natural unit of mass for the problem of the SHO (2)
is to take the mass of the oscillating particle to be the unit
mass for the problem. Mathematically, 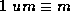 , or
equivalently
, or
equivalently 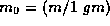 so that
so that 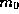 is just the numerical value
of the mass of the particle when measured in gm. Perhaps the most
intuitive unit of time for the problem would be the period of the
oscillator. However, this choice leads to a proliferation of factors
of
is just the numerical value
of the mass of the particle when measured in gm. Perhaps the most
intuitive unit of time for the problem would be the period of the
oscillator. However, this choice leads to a proliferation of factors
of 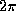 in formulae. A more natural choice is the amount of time it
takes for the oscillator to move through
in formulae. A more natural choice is the amount of time it
takes for the oscillator to move through 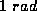 of phase, this will set
the value of the angular frequency within our unit system to be
of phase, this will set
the value of the angular frequency within our unit system to be
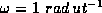 . From the general conversions in TABLE I, we see that
. From the general conversions in TABLE I, we see that 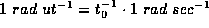 , and our choice thus sets the value
, and our choice thus sets the value 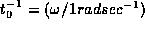 so that the inverse of the natural unit of time is the
numerical value of the frequency of the oscillator when measured in
the traditional unit of
so that the inverse of the natural unit of time is the
numerical value of the frequency of the oscillator when measured in
the traditional unit of 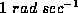 .
.
Having set um and ut, there remains
one basic unit to fix, the unit distance. Their also remains one final
experimental constant remains in the TISE for the SHO,  . It is
a general feature of dimensional analysis that choosing units for
three independent dimensions completely determines the new system of
units. In our case, the most convenient choice for the unit distance
is one where the numerical value of
. It is
a general feature of dimensional analysis that choosing units for
three independent dimensions completely determines the new system of
units. In our case, the most convenient choice for the unit distance
is one where the numerical value of  is
is 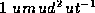 .
This fixes
.
This fixes 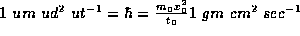 so that
so that 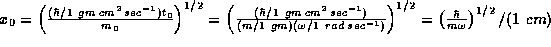 , which sets
, which sets 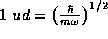 .
.
With the units for the basic dimensions determined, we
may now generate the basic units for all physical quantities by
inserting the choices we have made for the basic units, 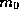 ,
,
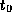 and
and 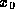 in the table above. The results of doing this we
summarize in the table below. Note that the results are always just
the only combination of powers of m,
in the table above. The results of doing this we
summarize in the table below. Note that the results are always just
the only combination of powers of m,  and
and  that have
the appropriate dimensions.
that have
the appropriate dimensions.

In our new system of units 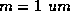 ,
, 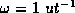 and
and 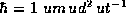 and the TISE, in the
position and momentum representations respectively, reads
and the TISE, in the
position and momentum representations respectively, reads
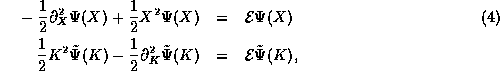
Here we
adopt the notation that quantities measured in our new system
of units always appear as either capital or calligraphic letters.
The conversion from quantities expressed in the natural units for this
problem and the standard cgs units is straight forward using Table
II. For instance, the traditional value of
energies E will just be the values we compute in our new units 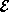 times the new unit of energy
times the new unit of energy 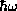 . Thus an energy of
. Thus an energy of
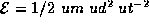 corresponds to an energy of
corresponds to an energy of 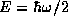 . It is common practice to drop writing our specialized
units and write simply
. It is common practice to drop writing our specialized
units and write simply 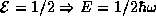 .
Similarly, a distance or position X=1 as measured in the new system
corresponds to
.
Similarly, a distance or position X=1 as measured in the new system
corresponds to 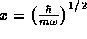 in the
traditional system.
in the
traditional system.
With the relation between basic quantities defined, the relationship
between functions may then be determined by physical reasoning. For
instance, the probability of finding the particle with a position in
the range with of traditional positions 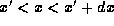 corresponds
to finding the position as measured in the new system in the range
corresponds
to finding the position as measured in the new system in the range
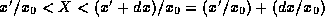 , thus
, thus 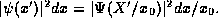 Hence, given
Hence, given 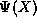 in the new
system we can always convert it to a traditional
in the new
system we can always convert it to a traditional 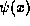 through
through
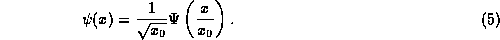



Next: Self-trasnform property of
Up: Dimensional Analysis
Previous: Motivation and General
Prof. Tomas Alberto Arias
Thu Oct 12 22:00:51 EDT 1995
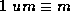 , or
equivalently
, or
equivalently 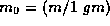 so that
so that 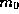 is just the numerical value
of the mass of the particle when measured in gm. Perhaps the most
intuitive unit of time for the problem would be the period of the
oscillator. However, this choice leads to a proliferation of factors
of
is just the numerical value
of the mass of the particle when measured in gm. Perhaps the most
intuitive unit of time for the problem would be the period of the
oscillator. However, this choice leads to a proliferation of factors
of 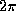 in formulae. A more natural choice is the amount of time it
takes for the oscillator to move through
in formulae. A more natural choice is the amount of time it
takes for the oscillator to move through 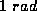 of phase, this will set
the value of the angular frequency within our unit system to be
of phase, this will set
the value of the angular frequency within our unit system to be
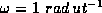 . From the general conversions in TABLE I, we see that
. From the general conversions in TABLE I, we see that 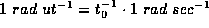 , and our choice thus sets the value
, and our choice thus sets the value 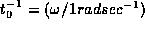 so that the inverse of the natural unit of time is the
numerical value of the frequency of the oscillator when measured in
the traditional unit of
so that the inverse of the natural unit of time is the
numerical value of the frequency of the oscillator when measured in
the traditional unit of 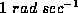 .
.
 . It is
a general feature of dimensional analysis that choosing units for
three independent dimensions completely determines the new system of
units. In our case, the most convenient choice for the unit distance
is one where the numerical value of
. It is
a general feature of dimensional analysis that choosing units for
three independent dimensions completely determines the new system of
units. In our case, the most convenient choice for the unit distance
is one where the numerical value of  is
is 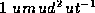 .
This fixes
.
This fixes 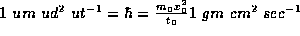 so that
so that 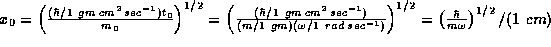 , which sets
, which sets 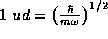 .
.
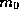 ,
,
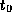 and
and 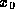 in the table above. The results of doing this we
summarize in the table below. Note that the results are always just
the only combination of powers of m,
in the table above. The results of doing this we
summarize in the table below. Note that the results are always just
the only combination of powers of m,  and
and  that have
the appropriate dimensions.
that have
the appropriate dimensions.

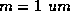 ,
, 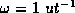 and
and 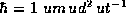 and the TISE, in the
position and momentum representations respectively, reads
and the TISE, in the
position and momentum representations respectively, reads
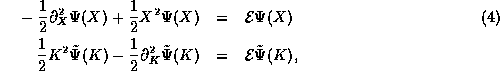
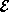 times the new unit of energy
times the new unit of energy 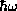 . Thus an energy of
. Thus an energy of
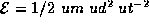 corresponds to an energy of
corresponds to an energy of 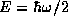 . It is common practice to drop writing our specialized
units and write simply
. It is common practice to drop writing our specialized
units and write simply 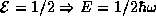 .
Similarly, a distance or position X=1 as measured in the new system
corresponds to
.
Similarly, a distance or position X=1 as measured in the new system
corresponds to 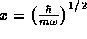 in the
traditional system.
in the
traditional system.
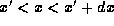 corresponds
to finding the position as measured in the new system in the range
corresponds
to finding the position as measured in the new system in the range
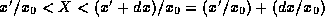 , thus
, thus 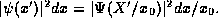 Hence, given
Hence, given 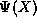 in the new
system we can always convert it to a traditional
in the new
system we can always convert it to a traditional 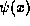 through
through