Massachusetts Institute of Technology
Department of Physics
Physics 8.04 Thu Oct 12 22:01:17 EDT 1995
The problem of the simple harmonic oscillator, where a particle of ass m moves in the potential
plays an important role in the understanding of a wide range of physical phenomena. Small oscillations of systems about their equilibrium configurations may be understood in the context of harmonic motions.
Vibrations of diatomic molecules provide perhaps the simplest example
of this. The potential energy as a function of the distance R
between two atoms in a diatomic molecule appears as in Figure 
.
For small motions about the equilibrium separation
(point of minimum energy), the
derivative of the potential 
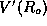is zero and
the potential is harmonic to second order,
Here we have defined 
so that 
where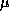 
is the reduced mass of the diatomic molecule, 
. In the spectra of diatomic molecules one
indeed finds the signature of a harmonic oscillator with frequency given by
the above formula. The vibrations of more complex systems such as
polyatomic molecules with hundreds of atoms or even solids with
atoms, may be decomposed into the oscillations of
collections of independent simple harmonic oscillators. The energy
quanta of these mechanical vibrations are referred to as
phonons.
The utility of the harmonic oscillator solutions goes beyond simple mechanical systems. As we learned from Planck's experience with cavity radiation, the oscillatory modes of electromagnetic radiation may be described as harmonic oscillators. We have already called the energy quanta of these oscillations photons. There are more esoteric examples as well. The tiny dipole moments in a magnetic solid may be set into oscillatory motions. The energy quanta of these oscillations are known as magnons. Finally, in particle physics, the processes by which particles are created and destroyed may be described using the same mathematics which describes the addition or removal, respectively, of energy quanta from a harmonic oscillator.
In this set of notes, we will discuss the wavefunctions and eigenenergies of the simple harmonic oscillator Hamiltonian,
This Hamiltonian gives rise to the following time independent Schrödinger equations, in the position and momentum representations respectively,
To find the eigenenergies and eigenstates of this system, we will proceed in three steps. First in Section 1, we will perform a dimensional analysis on the TISE for this problem. As we will see, dimensional analysis is a procedure by which many of the constants in an equation may be removed. This helps both to simplify the algebra and to foster insight into the deeper structure behind the equations. Next in Section 2, we will note that from the structure of the dimensionless TISE we can guess the solutions by inspection! The form of the solutions which we find in Section 2 will then lead us to a general form for the solution of the TISE for the SHO which will allow a full formal analysis of the states of the Hamiltonian (1) in Section 3.
