Although from our discussion in section (2) we would
strongly suspect that the solutions for the SHO are of the form
(6), the considerations of that section alone did not rule
out the possibility of other solutions. One way to keep our
search for solutions completely general but take advantage of our
insights from the previous section is to write the wavefunction in the
form of the product of a
Gaussian and an
unknown function 
, which we then expand in a Taylor series,
We may then derive an alternate equation for the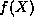 
. Because we
expect the solutions for this alternate equation to just be
polynomials, the hope is that this new equation will be easier to
solve than the original Schrödinger equation (4.
It is important that when writing the form (7), we have
not limited our search for solutions to the TISE in any way. We
see that this is so through the following argument. Given any
wavefunction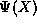 
which is a solution to the TISE, we may always
write it in the form (7) by simply defining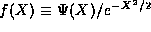 
. Written this way we see that 
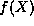may indeed
be expanded in a power series because it is the ratio (with non-zero
denominator) of two well-behaved analytic functions,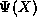 
and
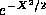. (We know that 
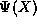is well-behaved and analytic
because it is the solution to the TISE with a potential which is
finite with all derivatives continuous.)
To derive the equation for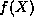 
, we
first take the appropriate derivatives of
,
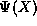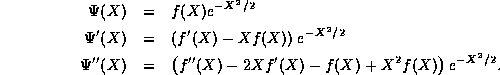
Inserting the result into the TISE (4) then gives
Equation (8) is now our equation for the function
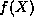, where we have defined a new parameter describing the energy
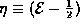so that 
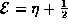. In
terms of traditional units the eigenenergies are
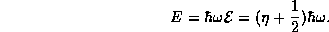
Note that Eq. (8) is a new eigenvalue equation, one
which determines the allowed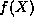 
which will turn out to be the
Hermite polynomials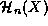 
.
To illustrate the use of this equation, we now use it to verify the
results that we have already. To see that
that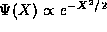 
is indeed a solution to the TISE and
that the corresponding energy is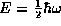 
, we
first identify that
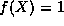and then insert this into (8),
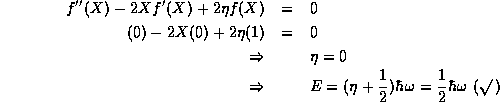
For the first excited state we have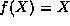 
, which we may also verify
as a solution with energy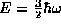 
by direct substitution,
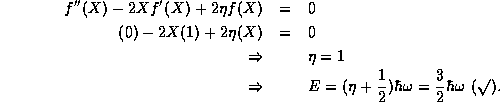
Finally, we might 'guess' at the solution for a new case and consider
the next state which must involve a quadratic term and a
constant term to make up for the error in taking a pure quadratic
term. The correct form turns out to be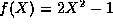 
, for then
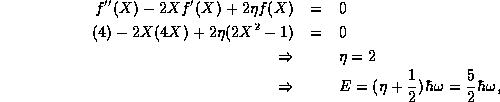
which we will find to represent the second excited state,
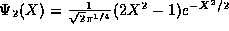(properly
normalized).
