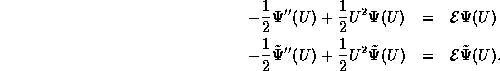
One of the benefits of performing the dimensional analysis is removing the clutter of the constants from (2) and highlighting the striking similarity between the position and momentum representation equations. If we rewrite the two equations in (4) using U as the dummy argument,
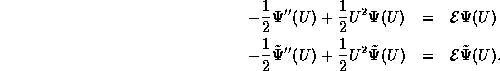
we see that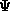 
and 
both solve precisely the same one dimensional
Schrödinger's equation with the same eigenvalue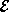 
! Because
there is at most one linearly independent solution for a given energy
for the TISE with finite potential in one dimension, we conclude that
and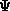 
must be the same up to a proportionality constant,
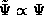. We know further that 
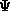and 
are related by the Fourier
transform,
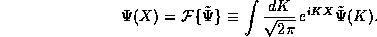
Thus we need consider as possible solutions to the TISE for the SHO only those functions which (up to an overall normalization factor) are their own Fourier transform.
The first such function which comes to mind in the Gaussian,
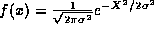. As we
learned in the notes on quantum states, the Fourier transform of this
function is just another Gaussian,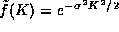 
.
For these to be the same function, we must have
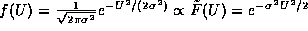so that
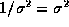and hence
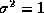. (If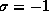 
the functions would be unnormalizable.)
Thus our first guess
for a possible solution to (4) is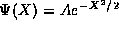 
. To verify this, we
insert our guess, or ansatz, into the TISE. It is convenient
to first compute the appropriate derivatives,
So that,
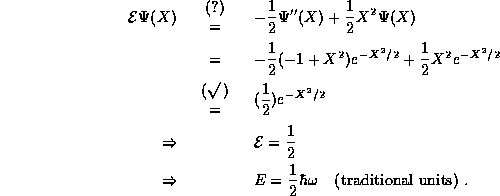
Indeed we have found a solution by simple inspection of the dimensionless TISE! (Note that there was no need to carry the normalization factor A though our analysis because the TISE is a linear equation and all of the factors of A cancel through.)
Recall that we found in our notes on the Heisenberg uncertainty
principle that
the absolute lower bound which the HUP places on the ground
state energy for a SHO is precisely this value of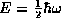 
. The state we have found must therefore the ground
state of the system,
(properly square-normalized).
This state does attain the absolute minimum energy allowed under the uncertainty principle and thus also represents the state of minimum uncertainty. From our analysis we have thus also identified the wavepacket of minimum uncertainty. It is the Gaussian wavepacket.
Having identified the ground state, we may generate other states from it using the observation that taking successive derivatives of a function generates successive factors of iK in its Fourier transform:
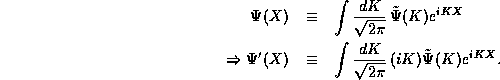
If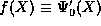 
, then 
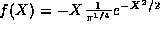but also 
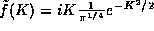! Once again,
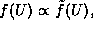and may have found yet another state,
To verify that we have indeed found
another state, we first compute the derivatives of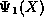 
,
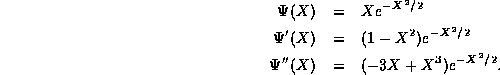
Inserting into the TISE,
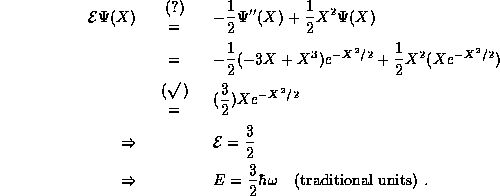
When properly normalized, this state is
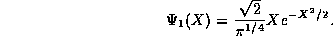
Unfortunately, simply taking yet another derivative will not work.
The basic properties of the fourier transform tell us that if
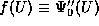then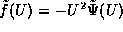 
, but we found
above that 
. This is not proportional to
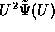but has an additional term proportional to 
.
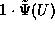One may develop a procedure
to deal with this issue and find a method for finding an algebraic
solution for the TISE for the SHO which does not require the direct
solution of any differential equations.
For now, we will take as our main lesson ,
the strong
suspicion that the eigenfunctions of the SHO are of the form of
polynomials times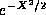 
, 
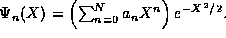As we shall see in the next section, this
ansatz is correct. The polynomials which multiply the Gaussian
factor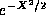 
are given a special name, the Hermite polynomials,
and the symbol 
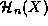. The solutions to the
Harmonic oscillator will turn out to be
where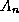 
is an appropriate normalization factor.
