
We now proceed to search for the general solution of the eigenvalue equation (8) in the form of power series,
After inserting this form into the eigenvalue equation for 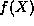 ,
we will generate, not surprisingly, an
eigenvalue equation, for the
,
we will generate, not surprisingly, an
eigenvalue equation, for the 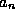 . This
equation at last will be one which we may solve easily by recursion.
. This
equation at last will be one which we may solve easily by recursion.
As before, it is useful to take the appropriate derivatives before inserting the general form (9) into the equation (8),
The form we now have for the first derivative is particularly convenient
because in (8) 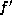 appears with a factor of X which will
combine with the factor of
appears with a factor of X which will
combine with the factor of 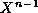 in the series in (11
to produce a net
factor of
in the series in (11
to produce a net
factor of  allowing us to combine terms in (8) easily.
Unfortunately, the same is not true of the above series for the second
derivative. To put the second derivative term on the same footing
with the other terms in (8), we should shift the indexing
of the sum by 2 so that the terms can combine. This procedure is
analogous to a change of variables when integrating,
allowing us to combine terms in (8) easily.
Unfortunately, the same is not true of the above series for the second
derivative. To put the second derivative term on the same footing
with the other terms in (8), we should shift the indexing
of the sum by 2 so that the terms can combine. This procedure is
analogous to a change of variables when integrating,
We are ready to substitute the series expansion for 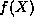 into (8).
Inserting (10,11,13) into (8), we find
into (8).
Inserting (10,11,13) into (8), we find
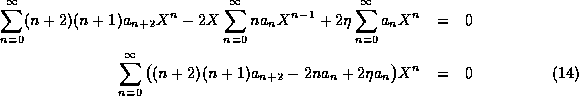
For the series to be identically zero, all of its terms must be zero separately and therefore we must have
This is the eigenvalue equation we expected for the 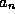 . Because
this equation describes a discrete
sequences of numbers (
. Because
this equation describes a discrete
sequences of numbers (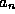 ) rather that a continuous function (such
as
) rather that a continuous function (such
as 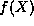 ), it is known as a finite difference eigenvalue equation.
), it is known as a finite difference eigenvalue equation.