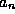 , reconstructing the
, reconstructing the
 and, finally, producing the wavefunctions
and, finally, producing the wavefunctions
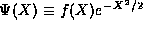 .
.
We now complete the series solution for the eigenvalue
equation by solving (15) for the 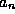 , reconstructing the
, reconstructing the
 and, finally, producing the wavefunctions
and, finally, producing the wavefunctions
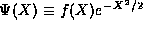 .
.
Equation (15) is solved by rewriting it as a linear recursion relation,
Applying (16) recursively for 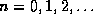 in
sequence, we find
in
sequence, we find
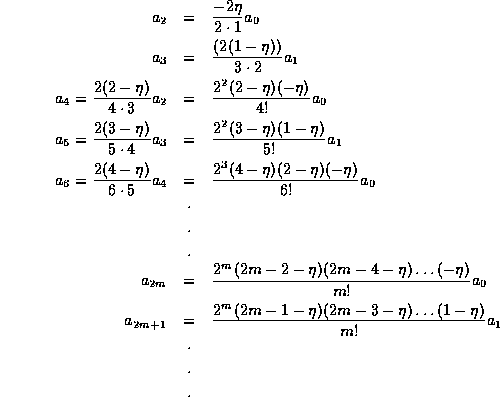
Note that in this case, the even and odd terms form independent
sequences so that we may write  as the sum of an even part
as the sum of an even part 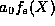 and an odd part
and an odd part 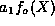 ,
,
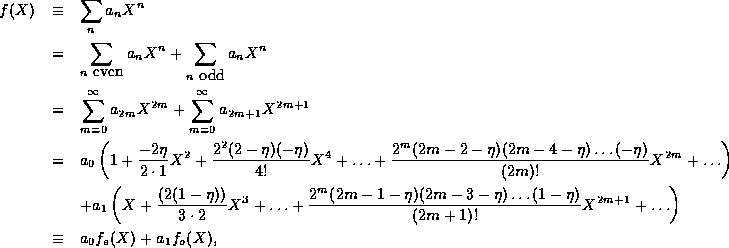
where 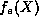 and
and 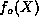 are even and odd functions of X
respectively. Note that the functions
are even and odd functions of X
respectively. Note that the functions 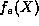 and
and 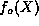 may be
generated according to the above formulas for any value of
may be
generated according to the above formulas for any value of 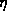 , the
parameter describing the energy.
, the
parameter describing the energy.
At last our solution is 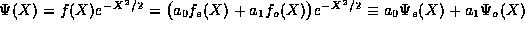 . At
this point is seems we
have identified two linearly independent solutions,
. At
this point is seems we
have identified two linearly independent solutions, 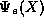 (even) and
(even) and 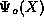 (odd) for every (continuous) value of the
energy parameter
(odd) for every (continuous) value of the
energy parameter 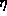 . We know that all of these
solutions which we have found cannot represent pure energy states of
the SHO. First, all SHO
states are bound (
. We know that all of these
solutions which we have found cannot represent pure energy states of
the SHO. First, all SHO
states are bound (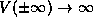 ) and bound states
exhibit a discrete, not continuous, spectrum. Second, we expect (in
one dimension) only a single physical state for each allowed
energy, but here we appear to have found two. There must therefore be
a physical reason for rejecting many of the solutions we have found.
) and bound states
exhibit a discrete, not continuous, spectrum. Second, we expect (in
one dimension) only a single physical state for each allowed
energy, but here we appear to have found two. There must therefore be
a physical reason for rejecting many of the solutions we have found.
The physical reason for rejecting some of these solutions is
clearly illustrated when we look at the two solutions corresponding to
the ground state of the harmonic oscillator,
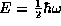 , or
, or 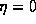 . From the
series solution we have
. From the
series solution we have
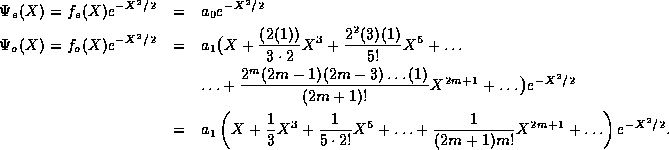
A plot of these two functions is provided in Figure 3.3.
While the even solution, 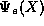 , is well behaved and decays into
the forbidden regions at |X|>1 while curving away from the x-axis,
the odd solution enters the forbidden region with too great of a
slope and thus begins to grow exponentially as
, is well behaved and decays into
the forbidden regions at |X|>1 while curving away from the x-axis,
the odd solution enters the forbidden region with too great of a
slope and thus begins to grow exponentially as
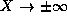 . As in the case of the square well,
because this function is not be normalizable, we reject it as
unphysical.
. As in the case of the square well,
because this function is not be normalizable, we reject it as
unphysical.
We could have anticipated this behavior analytically with out
resorting to a plot. The key observation is that only when the
series for 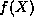 ``terminates'' and the coefficients became zero
after some point leaving only a polynomial, then the wave function
``terminates'' and the coefficients became zero
after some point leaving only a polynomial, then the wave function
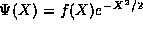 drops sufficiently rapidly for large X
that it is normalizable. If the series does not terminate, the
function
drops sufficiently rapidly for large X
that it is normalizable. If the series does not terminate, the
function 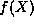 grows so rapidly with X that even after
multiplication by
grows so rapidly with X that even after
multiplication by 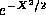 the wavefunction cannot be normalized.
In the next subsection we will proof that this is so. For now, we
will take this intuitively reasonable result as given.
the wavefunction cannot be normalized.
In the next subsection we will proof that this is so. For now, we
will take this intuitively reasonable result as given.
The form of the recursion (16) is such that the series
terminates only for 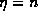 where n is a nonnegative integer. If
where n is a nonnegative integer. If
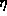 is not an integer, then neither
is not an integer, then neither 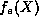 nor
nor 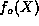 will
terminate, and neither the even or odd solution is normalizable or
physical. Thus we see that
will
terminate, and neither the even or odd solution is normalizable or
physical. Thus we see that 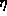 must be an integer. Moreover, if
must be an integer. Moreover, if
 is an even (odd) integer, the series for
is an even (odd) integer, the series for 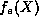 (
(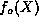 )
will terminate at the point where
)
will terminate at the point where 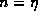 but the series for
but the series for 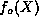 (
(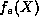 ) will not terminate because
) will not terminate because 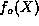 (
(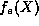 ) contains
terms only for odd (even) n. If
) contains
terms only for odd (even) n. If 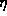 is even (odd), the only
allowable solution will be the finite polynomial
is even (odd), the only
allowable solution will be the finite polynomial 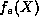 (
(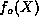 ).
Up to an overall normalization constant, the Hermite polynomials
are defined as these terminated
).
Up to an overall normalization constant, the Hermite polynomials
are defined as these terminated 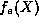 and
and 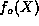 . Because
(8) is a linear equation, it does not determine the
overall normalization of the Hermite polynomials. By convention, this
normalization is set so that the highest order term in
. Because
(8) is a linear equation, it does not determine the
overall normalization of the Hermite polynomials. By convention, this
normalization is set so that the highest order term in  is
is
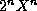 . Using this definition and the recursion
(16), we find the following for the first few Hermite
polynomials,
. Using this definition and the recursion
(16), we find the following for the first few Hermite
polynomials,

To sum up, we thus have,
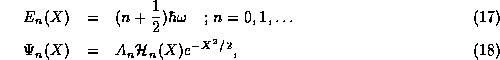
where, the 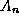 are normalization constants defined so that
are normalization constants defined so that 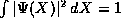 , which
can be show to
leave them with the values,
, which
can be show to
leave them with the values,

Note that these solutions also obey the rule that the 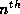 excited
state is even or odd according to the value of n and has n nodes.
excited
state is even or odd according to the value of n and has n nodes.