


Next: About this document
Up: Series solution for
Previous: Putting the pieces
In considering the physical admissibility of the solutions
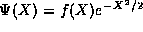 we first noted that if
we first noted that if 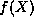 is a finite
polynomial that
is a finite
polynomial that 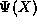 is normalizable because of the extremely
rapid fall of the Gaussian factor. We then assumed that if the
series for
is normalizable because of the extremely
rapid fall of the Gaussian factor. We then assumed that if the
series for 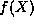 did not terminate, that the resulting
did not terminate, that the resulting 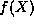 would
grow so rapidly that even the Gaussian decay of the factor
would
grow so rapidly that even the Gaussian decay of the factor
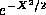 could not make
could not make 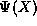 normalizable. In this
subsection, we shall investigate why this should be the case.
normalizable. In this
subsection, we shall investigate why this should be the case.
The key observation which we shall exploit is that for large n the
coefficients 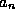 in the sequence defining
in the sequence defining 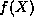 behave
much like
the terms in the expansion for
behave
much like
the terms in the expansion for 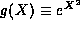 so that, for large
X,
so that, for large
X,  grows at least like
grows at least like 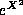 , so that not even
multiplication by
the Gaussian decay factor
, so that not even
multiplication by
the Gaussian decay factor 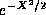 will render the wave function
normalizable. The basic similarity of the two expansions comes from
the behavior of the ratio of the
will render the wave function
normalizable. The basic similarity of the two expansions comes from
the behavior of the ratio of the 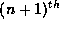 to the
to the 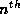 terms in
the sequence successive terms.
For
terms in
the sequence successive terms.
For  the ratio is
the ratio is
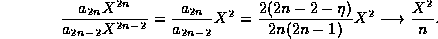
For 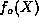 the ratio approaches the same limit,
the ratio approaches the same limit,
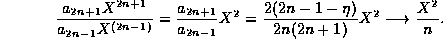
We find precisely the same limit in the case of our auxiliary
function, 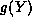 . For
. For
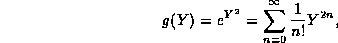
the ratio is
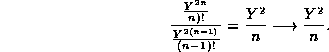
Note that the ratio of successive terms may be negative for small
values of n so that the terms in the series for the  may
alternate in sign. Because the ratio approaches a positive limit,
However, we are assured that for sufficiently large n, all terms
will be of the same sign. Moreover, because
may
alternate in sign. Because the ratio approaches a positive limit,
However, we are assured that for sufficiently large n, all terms
will be of the same sign. Moreover, because
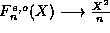 , we may find an N so that
for all n>N the ratio of successive terms in
, we may find an N so that
for all n>N the ratio of successive terms in 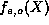 will
exceed
will
exceed 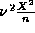 where
where 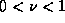 is any number between
zero and one. This is important because this is just the quantity
(
is any number between
zero and one. This is important because this is just the quantity
(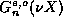 , which is the ratio of successive terms in
, which is the ratio of successive terms in 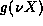 . If we now multiply
. If we now multiply 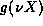 by a constant
by a constant 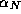 so that the
so that the
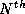 term of
term of 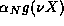 is equal in magnitude to the
is equal in magnitude to the
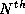 term of
term of 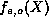 , this implies that all successive terms
in
, this implies that all successive terms
in 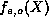 will exceed their counterparts in
will exceed their counterparts in 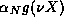 .
Because all of the terms in question are of the same sign, the
absolute value of the sum of all remaining terms in
.
Because all of the terms in question are of the same sign, the
absolute value of the sum of all remaining terms in 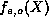 exceeds that of the associated terms in
exceeds that of the associated terms in 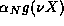 , which is
important because we know that g grows too fast to yield a
normalizable function. To complete the argument, let
, which is
important because we know that g grows too fast to yield a
normalizable function. To complete the argument, let  be the
sum of the first N terms in
be the
sum of the first N terms in 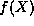 and
and 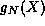 be the sum of the
first N terms in
be the sum of the
first N terms in 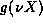 . Note that both
. Note that both 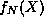 and
and 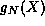 are finite polynomials. We have just shown that for every
are finite polynomials. We have just shown that for every 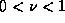 there exist a constant
there exist a constant 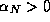 and integer N such that for all
X,
and integer N such that for all
X,
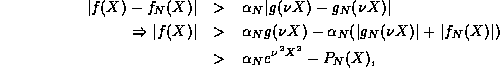
where 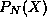 is a function which grows at most as quickly as an
is a function which grows at most as quickly as an
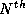 order polynomial. If we now consider the behavior of the
wave function at large values of X,
order polynomial. If we now consider the behavior of the
wave function at large values of X, 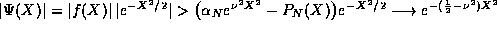 . (The limit of any
polynomial times a Gaussian factor is zero.) This statement is true
of any
. (The limit of any
polynomial times a Gaussian factor is zero.) This statement is true
of any 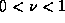 . For this to be true for
. For this to be true for 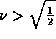 , we
see that, as long as the series for
, we
see that, as long as the series for 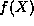 does not terminate, we must
have
does not terminate, we must
have 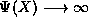 as
as  .
This completes the proof of our claim that we must reject all
solutions of
.
This completes the proof of our claim that we must reject all
solutions of 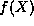 for which the series do not terminate and
culminates our power series analysis of the quantum states of the SHO.
for which the series do not terminate and
culminates our power series analysis of the quantum states of the SHO.



Next: About this document
Up: Series solution for
Previous: Putting the pieces
Prof. Tomas Alberto Arias
Thu Oct 12 22:00:51 EDT 1995
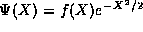 we first noted that if
we first noted that if 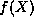 is a finite
polynomial that
is a finite
polynomial that 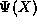 is normalizable because of the extremely
rapid fall of the Gaussian factor. We then assumed that if the
series for
is normalizable because of the extremely
rapid fall of the Gaussian factor. We then assumed that if the
series for 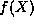 did not terminate, that the resulting
did not terminate, that the resulting 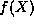 would
grow so rapidly that even the Gaussian decay of the factor
would
grow so rapidly that even the Gaussian decay of the factor
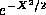 could not make
could not make 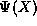 normalizable. In this
subsection, we shall investigate why this should be the case.
normalizable. In this
subsection, we shall investigate why this should be the case.
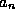 in the sequence defining
in the sequence defining 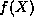 behave
much like
the terms in the expansion for
behave
much like
the terms in the expansion for 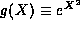 so that, for large
X,
so that, for large
X,  grows at least like
grows at least like 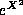 , so that not even
multiplication by
the Gaussian decay factor
, so that not even
multiplication by
the Gaussian decay factor 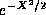 will render the wave function
normalizable. The basic similarity of the two expansions comes from
the behavior of the ratio of the
will render the wave function
normalizable. The basic similarity of the two expansions comes from
the behavior of the ratio of the 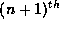 to the
to the 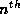 terms in
the sequence successive terms.
For
terms in
the sequence successive terms.
For  the ratio is
the ratio is
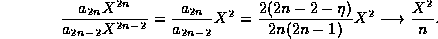
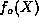 the ratio approaches the same limit,
the ratio approaches the same limit,
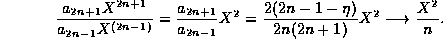
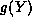 . For
. For 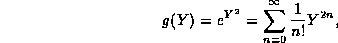
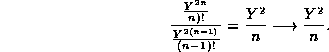
 may
alternate in sign. Because the ratio approaches a positive limit,
However, we are assured that for sufficiently large n, all terms
will be of the same sign. Moreover, because
may
alternate in sign. Because the ratio approaches a positive limit,
However, we are assured that for sufficiently large n, all terms
will be of the same sign. Moreover, because
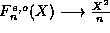 , we may find an N so that
for all n>N the ratio of successive terms in
, we may find an N so that
for all n>N the ratio of successive terms in 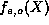 will
exceed
will
exceed 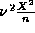 where
where 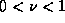 is any number between
zero and one. This is important because this is just the quantity
(
is any number between
zero and one. This is important because this is just the quantity
(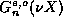 , which is the ratio of successive terms in
, which is the ratio of successive terms in 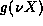 . If we now multiply
. If we now multiply 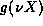 by a constant
by a constant 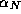 so that the
so that the
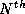 term of
term of 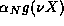 is equal in magnitude to the
is equal in magnitude to the
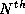 term of
term of 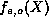 , this implies that all successive terms
in
, this implies that all successive terms
in 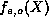 will exceed their counterparts in
will exceed their counterparts in 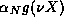 .
Because all of the terms in question are of the same sign, the
absolute value of the sum of all remaining terms in
.
Because all of the terms in question are of the same sign, the
absolute value of the sum of all remaining terms in 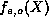 exceeds that of the associated terms in
exceeds that of the associated terms in 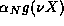 , which is
important because we know that g grows too fast to yield a
normalizable function. To complete the argument, let
, which is
important because we know that g grows too fast to yield a
normalizable function. To complete the argument, let  be the
sum of the first N terms in
be the
sum of the first N terms in 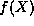 and
and 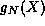 be the sum of the
first N terms in
be the sum of the
first N terms in 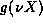 . Note that both
. Note that both 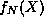 and
and 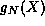 are finite polynomials. We have just shown that for every
are finite polynomials. We have just shown that for every 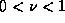 there exist a constant
there exist a constant 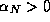 and integer N such that for all
X,
and integer N such that for all
X,
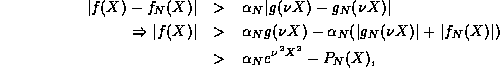
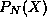 is a function which grows at most as quickly as an
is a function which grows at most as quickly as an
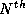 order polynomial. If we now consider the behavior of the
wave function at large values of X,
order polynomial. If we now consider the behavior of the
wave function at large values of X, 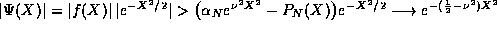 . (The limit of any
polynomial times a Gaussian factor is zero.) This statement is true
of any
. (The limit of any
polynomial times a Gaussian factor is zero.) This statement is true
of any 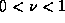 . For this to be true for
. For this to be true for 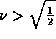 , we
see that, as long as the series for
, we
see that, as long as the series for 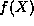 does not terminate, we must
have
does not terminate, we must
have 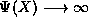 as
as  .
This completes the proof of our claim that we must reject all
solutions of
.
This completes the proof of our claim that we must reject all
solutions of 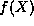 for which the series do not terminate and
culminates our power series analysis of the quantum states of the SHO.
for which the series do not terminate and
culminates our power series analysis of the quantum states of the SHO.