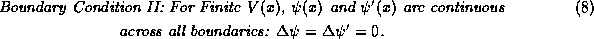Next: Region II
Up: Finite Square Well
Previous: Region I
While we know that any physical state obeys the TISE in each of the
three regions I, II and III, we must be careful in how we connect our
solutions across the interfaces at x=-a and x=a. Because
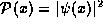 is a physically measurable quantity we expect it
and thus
is a physically measurable quantity we expect it
and thus 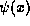 always to be continuous. It is not necessary to
add this as an additional physical requirement, because this
continuity is a consequence of the TISE. Recall that the finite
square well potential represents an idealization of a smooth potential
which happens to vary extremely rapidly at the interfaces between the
regions. In all physical cases where the potential is ``smooth''
(continuous with all of its derivatives continuous, a so called
``
always to be continuous. It is not necessary to
add this as an additional physical requirement, because this
continuity is a consequence of the TISE. Recall that the finite
square well potential represents an idealization of a smooth potential
which happens to vary extremely rapidly at the interfaces between the
regions. In all physical cases where the potential is ``smooth''
(continuous with all of its derivatives continuous, a so called
`` '' function), the solutions to the TISE will also be
smooth. All we must then determine is the behavior of the solutions
of the TISE, as we make the walls of the well steeper and steeper.
'' function), the solutions to the TISE will also be
smooth. All we must then determine is the behavior of the solutions
of the TISE, as we make the walls of the well steeper and steeper.
The best way to predict this behavior of the wavefunctions is to apply
the mean value theorem
of calculus. The mean value theorem states that for any function
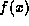 whose derivative
exists over the range between two points
whose derivative
exists over the range between two points 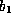 and
and 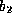 , there exists a
third
point c between
, there exists a
third
point c between 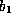 and
and 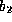 for which
for which
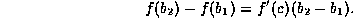
To apply this theorem in our case, we take
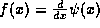 in (2). In
any case where
in (2). In
any case where 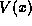 is continuous (although perhaps very steep) for
any two points
is continuous (although perhaps very steep) for
any two points 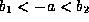 straddling the interface at x=-a,
straddling the interface at x=-a,
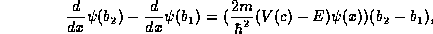
for some point c in the range 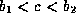 .
Because
.
Because 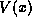 remains finite in the range
remains finite in the range 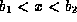 , as we take
the limit
, as we take
the limit 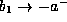 and
and 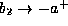 , the left hand side of the
above equation will
approach zero and thus
, the left hand side of the
above equation will
approach zero and thus
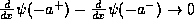 , and we have
proven that the derivative
, and we have
proven that the derivative 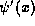 remains continuous even if the
potential possesses a finite discontinuity.
remains continuous even if the
potential possesses a finite discontinuity.
A similar argument may be applied to
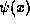 to show that whenever
to show that whenever 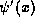 is finite, the wavefunction
itself is also continuous. Taken together, these two facts give our
second boundary condition:
is finite, the wavefunction
itself is also continuous. Taken together, these two facts give our
second boundary condition:
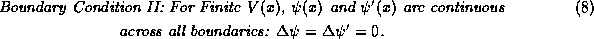
This tells us how to connect solutions across the interface at x=-a
and continue our solution from region I into region II.



Next: Region II
Up: Finite Square Well
Previous: Region I
Prof. Tomas Alberto Arias
Thu Oct 12 21:20:39 EDT 1995
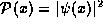 is a physically measurable quantity we expect it
and thus
is a physically measurable quantity we expect it
and thus 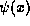 always to be continuous. It is not necessary to
add this as an additional physical requirement, because this
continuity is a consequence of the TISE. Recall that the finite
square well potential represents an idealization of a smooth potential
which happens to vary extremely rapidly at the interfaces between the
regions. In all physical cases where the potential is ``smooth''
(continuous with all of its derivatives continuous, a so called
``
always to be continuous. It is not necessary to
add this as an additional physical requirement, because this
continuity is a consequence of the TISE. Recall that the finite
square well potential represents an idealization of a smooth potential
which happens to vary extremely rapidly at the interfaces between the
regions. In all physical cases where the potential is ``smooth''
(continuous with all of its derivatives continuous, a so called
``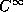 '' function), the solutions to the TISE will also be
smooth. All we must then determine is the behavior of the solutions
of the TISE, as we make the walls of the well steeper and steeper.
'' function), the solutions to the TISE will also be
smooth. All we must then determine is the behavior of the solutions
of the TISE, as we make the walls of the well steeper and steeper.
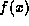 whose derivative
exists over the range between two points
whose derivative
exists over the range between two points 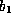 and
and 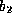 , there exists a
third
point c between
, there exists a
third
point c between 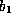 and
and 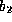 for which
for which
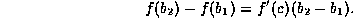
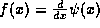 in (
in (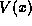 is continuous (although perhaps very steep) for
any two points
is continuous (although perhaps very steep) for
any two points 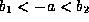 straddling the interface at x=-a,
straddling the interface at x=-a,
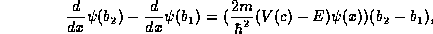
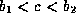 .
Because
.
Because 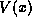 remains finite in the range
remains finite in the range 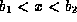 , as we take
the limit
, as we take
the limit 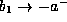 and
and 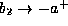 , the left hand side of the
above equation will
approach zero and thus
, the left hand side of the
above equation will
approach zero and thus
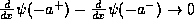 , and we have
proven that the derivative
, and we have
proven that the derivative 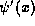 remains continuous even if the
potential possesses a finite discontinuity.
remains continuous even if the
potential possesses a finite discontinuity.
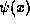 to show that whenever
to show that whenever 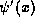 is finite, the wavefunction
itself is also continuous. Taken together, these two facts give our
second boundary condition:
is finite, the wavefunction
itself is also continuous. Taken together, these two facts give our
second boundary condition: