The notion of a particle following a Newtonian trajectory involves the
concept of of a localized object following a well defined path in
space. This notion is not unfamiliar in the theory of waves. It
corresponds to the wave theory notion of a wave packet. In wave
theory the superposition of a packet or group of waves waves with
slightly different wavelengths can produce a wave which is localized
in space. With an appropriate combination, the center of the group of
waves will travel with an average overall velocity known as the
group velocity. The two descriptions can be reconciled and will
correspond provided that the group velocity 
in the wave
description and the particle velocity v along the Newtonian
trajectory description can be made to always agree!
As an example of a wave packet, consider the combination of two waves
and
Defining the phases
and the phase difference
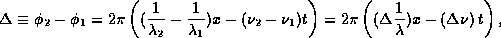
we analyze the superposition of these waves as
where 
and 
. If the waves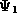 
and
are close in frequency, we see that the new wave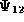 
looks much like the original waves 
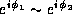, but
for a phase shift 
and a modulation in amplitude A. (See
figures below.)
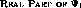
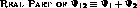
Note that the modulation in amplitude
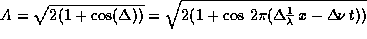, tends to localize the wave group 
into regions which travel at a velocity 
given by
. We did not achieve perfect
localization with this wave ``group'' of two waves because we used so
few waves. In general, the more waves that make up the group, the
better it can be localized. When dealing with waves, there is
generally a relationship between the frequency and wavelength of the
waves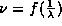 
. This is known as the dispersion
relationship and is a a basic property of each type of wave we
encounter. Although here we only used two waves in our group, one can
give a similar argument in the general case to show that even when
combining many waves, as long as their frequencies and wavelengths
fall in a narrow interval so that 
, then
which you may also see sometime written
where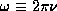 
and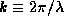 
.
