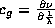 equal the Newtonian particle
velocity v. (
equal the Newtonian particle
velocity v. ( .) We also have from the
experiments the empirical observation (1) that
.) We also have from the
experiments the empirical observation (1) that
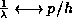 . Substituting these correspondences
in (4) leaves
. Substituting these correspondences
in (4) leaves
To achieve correspondence between the two descriptions, we would now
like to insist that the group velocity given by 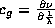 equal the Newtonian particle
velocity v. (
equal the Newtonian particle
velocity v. ( .) We also have from the
experiments the empirical observation (1) that
.) We also have from the
experiments the empirical observation (1) that
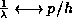 . Substituting these correspondences
in (4) leaves
. Substituting these correspondences
in (4) leaves
which relates the velocity of a particle on a Newtonian trajectory to
the derivative of some as yet unspecified Newtonian quantity (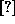 )
with respect to the particle's momentum. To complete the
correspondence, we must identify a derivative relationship like this
from classical Newtonian mechanics. Such a relation is well known in
advanced mechanics and is known as one of the two canonical equations
of motion of Hamilton.
)
with respect to the particle's momentum. To complete the
correspondence, we must identify a derivative relationship like this
from classical Newtonian mechanics. Such a relation is well known in
advanced mechanics and is known as one of the two canonical equations
of motion of Hamilton.
To derive the relationship we need, we use only the basic concepts of
the conservation of momentum and of energy. Conservation of momentum
tells us that if we apply an external force 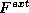 to a particle in
motion along a trajectory, then the momentum of the particle must
change according to
to a particle in
motion along a trajectory, then the momentum of the particle must
change according to
As the momentum of the particle changes, so will its energy. In this
derivation, it is useful for us to write the energy of a particle as a
function of its momentum, rather than the more familiar procedure of
writing the energy as a function of the velocity of the particle.
This form is generally more useful because it relates two conserved
quantities. Writing the energy this way is so useful, in fact, that
this form is given a special name in honor of Hamilton. It is called the
``Hamiltonian'' and by convention is written with the letter H,
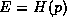 . In this argument, we will leave
. In this argument, we will leave 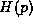 arbitrary.
It may take the usual form used in classical mechanics,
arbitrary.
It may take the usual form used in classical mechanics,
or the relativistic form we used when studying Compton scattering
or the energy-momentum relationship for a photon
or some other mysterious form we have not yet encountered.
With the energy written in this special way, the energy of our
particle will vary with the momentum 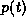 through the relationship
through the relationship
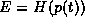 . The energy of the particle thus changes at the rate
. The energy of the particle thus changes at the rate
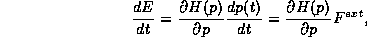
where we have used Eq. (6) to relate the force and the
rate of change of the momentum.
Applying the law of the conservation of energy, this rate of change of
energy of the particle along its trajectory must also must be the
rate at which the external force  does work on the particle,
does work on the particle,
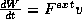 . We thus have
. We thus have
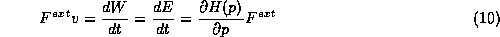
As so we conclude that, in general
This is easily verified in the cases above. For the classical particle (7),

For the photon (9)

The relativistic case (8) involves a bit more work, but the relation
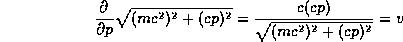
may be solved for p in terms of v to give the more familiar
