In scattering theory the most natural choice of normalization is that
the incoming ``source'' beam carry one particle per unit time. Note
that according to 3, such a beam which carries a unit
current, to the right or left respectively, always has the form
. To produce a solution with this
normalization of the incoming beam, we may simply
multiplying any general solution of the form 11
through by the factor 
to produce
where 
and 
. Note that some extra care has
been taken with the transmitted term to write it also in terms of a
beam carrying unit current, so that all three beams of particles,
source, reflected and transmitted are written a unit currents, with
perhaps some prefactors attached. These prefactors have very simple
physical interpretations and are thus given a special name. The
factors r(k) and t(k) are called the quantum amplitudes for
reflection and transmission, respectively.
Note that right-incident solutions, which we associate with values of k;SPMlt;0, should also be written in this special normalized form,
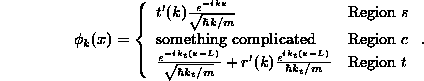
Throughout the rest of these notes, we will consider problems with particles incident from the left and thus use left-incident boundary conditions. All results are easily generalized to the right-incident case by reflecting the problem about the point x=L/2.
