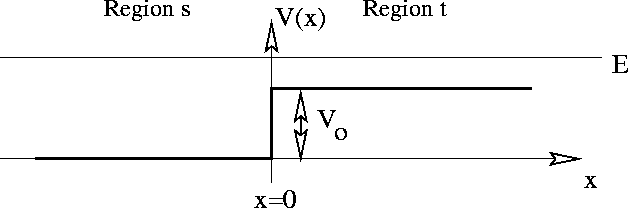
Figure 1: A potential with no bound states
So far, we have dealt with bound states, those stationary states where a particle has vanishing probability of being found at infinite distance. As we noted in our analysis of the square well, not all stationary states in a potential are bound. The potential in Figure 1, for instance, has no bound states.

Figure 1: A potential with no bound states
For any E ;SPMgt; 0, the particle has enough energy to exist classically at infinitely large distances to the left. The wave function in this region will be of the simple, non-decaying oscillatory form associated with classically allowed regions. The particle is not ``bound'' to any finite region about x=0. A complete understanding of quantum mechanics must include dealing with such unbound states. Such states are referred to as scattering states and are the subject of this set of lecture notes.
The solutions of the TISE answer two very important questions about a system. First, they determine the values which will be found in measurements of the energy of a system. Second, the time evolution of the state of a system may be written as a superposition of solutions to the TISE with the appropriate time dependent phases attached. For scattering states, the question of the allowed energies has a simple answer. In Section 3.2, we discuss how all values of energy in the scattering range of the spectrum are allowed. We will then proceed to spend most of our effort addressing the issue of the time evolution of the scattering states of the system.
Because we are no longer dealing with bound states, the time evolution of a system is no longer restricted to a probability distribution which sloshes back and forth in a confined region of space. In Figure 2 we show an example of the typical time evolution of scattering states. The figure shows the time evolution of the spatial probability distribution of finding a particle subjected to the potential of Figure 1. These distributions were determined by numerical integration of the Time Dependent Schrödinger Equation.
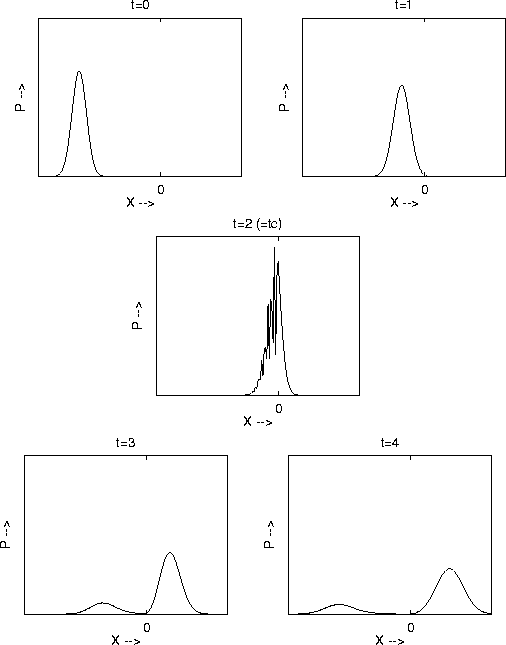
Figure 2: Example of time evolution of a particle approaching a
potential step
The figure shows that repeated measurements of the position of the particle at time t=0 yield a Gaussian distribution centered to the left of the origin x=0. The initial state of the particle has a non-zero average velocity in the +x direction. At time t=1, the center of the distribution has shifted to the right. During the intervening interval the distribution has spread in accordance with the Heisenberg Uncertainty Principle.
As time progress to t=2, the center of the packet has reached the
step. This time we shall refer to as ![]() , the time of the
collision. At time t=3, after the collision, the particle is no
longer likely to be found at the step, and the probability
distribution now takes on two peaks, one to the left and one to the
right of the step. As time progresses from t=3 to t=4 , the final
behavior of the probability distribution is evident. The two peaks in
the distribution now move away from the step, spreading in accordance
with the HUP.
, the time of the
collision. At time t=3, after the collision, the particle is no
longer likely to be found at the step, and the probability
distribution now takes on two peaks, one to the left and one to the
right of the step. As time progresses from t=3 to t=4 , the final
behavior of the probability distribution is evident. The two peaks in
the distribution now move away from the step, spreading in accordance
with the HUP.
In interpreting these results, it is important to keep in mind that
the particle has not split into two parts which then move either
to the left or right, it is merely the probability distribution
which has split. Repeated experiments will show that after the
collision at ![]() , the entire particle randomly either continues
forward (is transmitted by the step) or reverses course and
returns along their original path (is ``reflected'' by the
step). The probability of reflection or transmission is in direct
proportion to the areas of the two peaks moving away from the step
after the collision.
, the entire particle randomly either continues
forward (is transmitted by the step) or reverses course and
returns along their original path (is ``reflected'' by the
step). The probability of reflection or transmission is in direct
proportion to the areas of the two peaks moving away from the step
after the collision.
There are two more subtle effects of interest which we may study. There may be a delay of the scattered packets in the region of the step before they emerge. This delay if often supposed in science fiction stories to be zero during quantum tunneling events, thus allowing faster than light travel. It is also possible that the interaction with the step induces an additional spreading in the reflected and transmitted packets above and beyond what we normally expect for a packet propagating in free space. We will study this effect as well.
We will begin our discussion in in Section 2 with a full discussion of the simplest class of scattering states, particles propagating in free space (V(x)=0). Although, the solution in this case is the familiar spreading wave packet, we will take a fresh look at the problem. In Section 3 we will develop the general theory of scattering, and finally, in Section 4 we will apply our general theory to the specific the problem of scattering from the potential step in Figure 1.