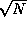The experimental evidence (G.I. Taylor, Davisson-Germer and others) we have considered indicates that natural phenomena take place as a series of many small discrete events occurring randomly but at a well defined overall random rate described by the square of a quantum probability amplitude. Quantum theory is concerned with the proper description of phenomena and thus intimately involves statistical averages. A full review of statistics is beyond the scope of this course. Fortunately, for our purposes, we need concern ourselves only with the most basic concepts of the random variable, average, variance/standard deviation and correlation/independence.
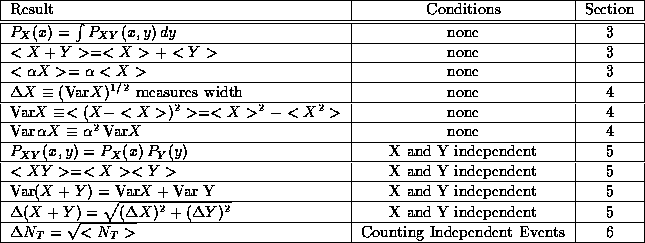
The results we shall derive in sections (2--5)
are summarized in the table below. If you are comfortable with these
formulas, feel free to skip the corresponding sections. Be sure to
read section (6), however, where we apply these results
to the spreading of a wave packet propagating in free space and to
prove the result quoted in class that if one expects N photons in a
given time interval, that the fluctuations in the actual number of
photons received will be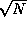 
. Also, we have some nice plots of
probability distributions and their mathematically defined widths in
section (4).
TABLE I: BASIC STATISTICAL RESULTS REVIEWED IN THIS NOTE
