


Next: Poisson(Counting) Statistics
Up: Applications
Previous: Applications
Suppose we have an experiment which produces a probability wave packet
describing a particle of mass m in free space. At time t=0, the
packer has a width 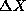 centered about <X> and travels at a
velocity <V>. By the uncertainty principle, we know that there is
an uncertainty in the momentum of the packet exceeding
centered about <X> and travels at a
velocity <V>. By the uncertainty principle, we know that there is
an uncertainty in the momentum of the packet exceeding 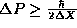 . Let us suppose that we begin with a packet
with the absolute minimum uncertainty. (We will be precise here with
the uncertainty principle because we are now using precise
mathematical definitions for
. Let us suppose that we begin with a packet
with the absolute minimum uncertainty. (We will be precise here with
the uncertainty principle because we are now using precise
mathematical definitions for 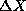 and
and 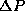 and because we
later will be able to compare our result here with a calculation using
the full formal wave theory.) Associated with the uncertainty in
momentum, there is also an uncertainty in the velocity of the
particle,
and because we
later will be able to compare our result here with a calculation using
the full formal wave theory.) Associated with the uncertainty in
momentum, there is also an uncertainty in the velocity of the
particle, 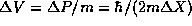 .
.
Because we are in free space and there is no force to change the
velocity of the particle, if we wait a time t>0 the velocity of the
particle will not change

and its new position will be given by the usual formula
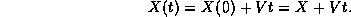
The uncertainty (standard deviation) in  now comes from
uncertainties both in X and V. Assuming that X and V are not
correlated and are independent, we then have
now comes from
uncertainties both in X and V. Assuming that X and V are not
correlated and are independent, we then have
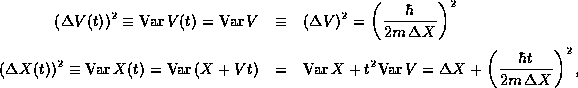
So that,
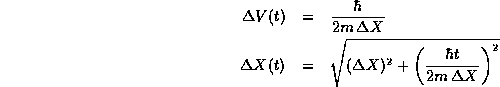
Note that  does not change with time as the packet
spreads because there is no force acting to change the velocity of the
particle in each measurement. This does not violate the uncertainty
principle because
does not change with time as the packet
spreads because there is no force acting to change the velocity of the
particle in each measurement. This does not violate the uncertainty
principle because 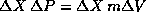 ,
which grows with time, continues to exceed
,
which grows with time, continues to exceed 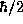 . The uncertainty
principle is an inequality, not an equality!
. The uncertainty
principle is an inequality, not an equality!
Prof. Tomas Alberto Arias
Wed Oct 11 13:59:29 EDT 1995
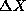 centered about <X> and travels at a
velocity <V>. By the uncertainty principle, we know that there is
an uncertainty in the momentum of the packet exceeding
centered about <X> and travels at a
velocity <V>. By the uncertainty principle, we know that there is
an uncertainty in the momentum of the packet exceeding 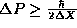 . Let us suppose that we begin with a packet
with the absolute minimum uncertainty. (We will be precise here with
the uncertainty principle because we are now using precise
mathematical definitions for
. Let us suppose that we begin with a packet
with the absolute minimum uncertainty. (We will be precise here with
the uncertainty principle because we are now using precise
mathematical definitions for 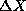 and
and 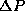 and because we
later will be able to compare our result here with a calculation using
the full formal wave theory.) Associated with the uncertainty in
momentum, there is also an uncertainty in the velocity of the
particle,
and because we
later will be able to compare our result here with a calculation using
the full formal wave theory.) Associated with the uncertainty in
momentum, there is also an uncertainty in the velocity of the
particle, 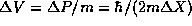 .
.

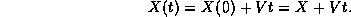
 now comes from
uncertainties both in X and V. Assuming that X and V are not
correlated and are independent, we then have
now comes from
uncertainties both in X and V. Assuming that X and V are not
correlated and are independent, we then have
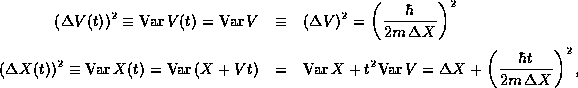
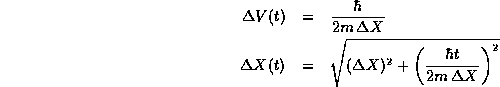
 does not change with time as the packet
spreads because there is no force acting to change the velocity of the
particle in each measurement. This does not violate the uncertainty
principle because
does not change with time as the packet
spreads because there is no force acting to change the velocity of the
particle in each measurement. This does not violate the uncertainty
principle because 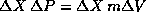 ,
which grows with time, continues to exceed
,
which grows with time, continues to exceed 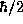 . The uncertainty
principle is an inequality, not an equality!
. The uncertainty
principle is an inequality, not an equality!